Примеры решения задач с векторами

Запись $\overline{a}=(5 ;-2)$ означает, что вектор $\overline{a}$ имеет следующие координаты: абсцисса равна 5, ордината равна -2.

Задание. Заданы векторы $\overline{a}=(-3 ; 5)$ и $\overline{b}=(0 ;-1)$. Найти координаты вектора $\overline{c}=\overline{a}+\overline{b}$

Решение. $\overline{c}=\overline{a}+\overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$

Задание. Вектор $\overline{a}=(3 ;-2)$. Найти координаты вектора 2$\overline{a}$

Решение. $2 \overline{a}=2 \cdot(3 ;-2)=(2 \cdot 3 ; 2 \cdot(-2))=(6 ;-4)$

Задание. Найти координаты вектора $\overline{A B}$, если $A(-4 ; 2), B(1 ;-3)$

Решение. $\overline{A B}=(1-(-4) ;-3-2)=(5 ;-5)$

Задание. Найти длину вектора $\overline{a}=(-4 ; 3)$

Решение. Используя формулу, получаем:

$|\overline{a}|=\sqrt{(-4)^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}=5$

Задание. Найти длину вектора $\overline{a}=(1 ; 0 ;-4)$

Решение. Используя формулу, получаем:

$|\overline{a}|=\sqrt{1^{2}+0^{2}+(-4)^{2}}=\sqrt{1+0+16}=\sqrt{17}$

Задание. Известно, что скалярное произведение двух векторов $(\overline{a} ; \overline{b})=2$, а их длины $|\overline{a}|=2,|\overline{b}|=2$. Найти угол между векторами $\overline{a}$ и $\overline{b}$.

Решение. Косинус искомого угла:

$$\cos (\bar{a}, \bar{b})=\frac{(\bar{a} ; \bar{b})}{|\bar{a}| \cdot|\bar{b}|}=\frac{2}{2 \cdot 2}=\frac{1}{2} \Rightarrow(\bar{a}, \bar{b})=60^{\circ}$$

Задание. Найти угол между векторами $\overline{a}=(1 ; \sqrt{3})$ и $\overline{b}=(1 ; 0)$

Решение. Косинус искомого угла

$$\cos (\bar{a}, \bar{b})=\frac{1 \cdot 1+\sqrt{3} \cdot 0}{\sqrt{1^{2}+(\sqrt{3})^{2}} \cdot \sqrt{1^{2}+0^{2}}}=\frac{1}{2}$$ $$(\bar{a}, \bar{b})=\arccos \frac{1}{2}=60^{\circ}$$

Задание. Найти угол между векторами $\overline{a}=(1 ; 3)$ и $\overline{b}=(2 ; 1)$

Решение. Косинус искомого угла:

$$\cos (\bar{a}, \bar{b})=\frac{1 \cdot 2+3 \cdot 1}{\sqrt{1^{2}+3^{2}} \cdot \sqrt{2^{2}+1^{2}}}=\frac{5}{\sqrt{10} \cdot \sqrt{5}}=\sqrt{\frac{1}{2}}=\frac{\sqrt{2}}{2}$$ $$(\bar{a}, \bar{b})=\arccos \frac{\sqrt{2}}{2}=45^{\circ}$$

Задание. Зная разложения вектора $\overline{a}$ по базисной системе векторов: $\overline{a}=3 \overline{i}-\overline{k}$, записать координаты этого вектора в пространстве.

Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что $\overline{a}=3 \overline{i}-0 \cdot \overline{j}-\overline{k}$, получаем, что $\overline{a}=(3 ; 0 ;-1)$

Задание. Вектор $\overline{a}$ задан своими координатами: $\overline{a}=(2 ;-1 ; 5)$. Записать разложение данного вектора по ортам осей координат.

Решение. Координаты вектора - это коэффициенты при ортах координатных осей в разложении вектора по базисной системе векторов, поэтому искомое разложение:

$\overline{a}=2 \overline{i}-\overline{j}+5 \overline{k}$

Задание. Вычислить скалярное произведение векторов $\overline{a}$ и $\overline{b}$ , если их длины соответственно равны 2 и 3, а угол между ними 60°.

Решение. Так как из условия $|\overline{a}|=2$, $|\overline{b}|=3$, а 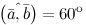, то

$\overline{a} \cdot \overline{b}=(\overline{a}, \overline{b})=2 \cdot 3 \cdot \cos 60^{\circ}=6 \cdot \frac{1}{2}=3$

Задание. Найти скалярное произведение векторов $\overline{a}=(3 ;-1)$ и $\overline{b}=(-2 ; 7)$

Решение. Скалярное произведение

$\overline{a} \overline{b}=3 \cdot(-2)+(-1) \cdot 7=-6-7=-13$

Задание. Найти векторное произведение векторов $\overline{a}=(6 ; 7 ; 10)$ и $\overline{b}=(8 ; 5 ; 9)$

Решение. Составляем определитель и вычисляем его:

$\overline{a} \times \overline{b}=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {6} & {7} & {10} \\ {8} & {5} & {9}\end{array}\right|=\overline{i} \left| \begin{array}{cc}{7} & {10} \\ {5} & {9}\end{array}\right|-\overline{j} \left| \begin{array}{cc}{6} & {10} \\ {8} & {9}\end{array}\right|+\overline{k} \left| \begin{array}{cc}{6} & {7} \\ {8} & {5}\end{array}\right|=$

$=\overline{i}(7 \cdot 9-5 \cdot 10)-\overline{j}(6 \cdot 9-8 \cdot 10)+\overline{k}(6 \cdot 5-8 \cdot 7)=$

$=13 \overline{i}+26 \overline{j}-26 \overline{k}=(13 ; 26 ;-26)$

Задание. Вычислить объем пирамиды, построенной на векторах $\overline{a}=(2 ; 3 ; 5)$, $\overline{b}=(1 ; 4 ; 4)$, $\overline{c}=(3 ; 5 ; 7)$

Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов $\overline{a}$, $\overline{b}$ и $\overline{c}$:

$(\overline{a}, \overline{b}, \overline{c})=\left| \begin{array}{lll}{2} & {3} & {5} \\ {1} & {4} & {4} \\ {3} & {5} & {7}\end{array}\right|=2 \cdot 4 \cdot 7+1 \cdot 5 \cdot 5+3 \cdot 4 \cdot 3-$

$-3 \cdot 4 \cdot 5-5 \cdot 4 \cdot 2-1 \cdot 3 \cdot 7=-4$

$$V_{пир}=\frac{1}{6}|(\overline{a}, \overline{b}, \overline{c})|=\frac{1}{6} \cdot 4=\frac{2}{3}$$