Скалярным произведением двух ненулевых векторов $\overline{a}$ и $\overline{b}$ называется число, равное произведению длин этих векторов на косинус угла между ними:
$$\bar{a} \bar{b}=\bar{a} \cdot \bar{b}=(\bar{a}, \bar{b})=|\bar{a}||\bar{b}| \cos (\bar{a}, \bar{b})$$Содержание:
Определение
Пример
Задание. Вычислить скалярное произведение векторов $\overline{a}$ и $\overline{b}$ , если их длины соответственно равны 2 и 3, а угол между ними 60°.
Решение. Так как из условия $|\overline{a}|=2$, $|\overline{b}|=3$, а $(\bar{a}, \bar{b})$, то
$\overline{a} \cdot \overline{b}=(\overline{a}, \overline{b})=2 \cdot 3 \cdot \cos 60^{\circ}=6 \cdot \frac{1}{2}=3$
Если хотя бы один из векторов $\overline{a}$ или $\overline{b}$ равен нулевому вектору, то $(\overline{a}, \overline{b})=0$.
Свойства скалярного произведения:
1 $(\overline{a}, \overline{b})=(\overline{b}, \overline{a})$ - симметричность.
2 $(\overline{a}, \overline{a})=|\overline{a}|^{2}$. Обозначается $(\overline{a}, \overline{a})=\overline{a}^{2}$ и называется скалярный квадрат.
3 Если $\overline{a} \neq \overline{0}$, то 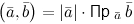
4 Если $\overline{a} \neq \overline{0}$ и $\overline{b} \neq \overline{0}$ и $(\overline{a}, \overline{b})=0$, то $\overline{a} \perp \overline{b}$. Верно и обратное утверждение.
5 $(\overline{a}+\overline{b}, \overline{c})=(\overline{a}, \overline{c})+(\overline{b}, \overline{c})$
6 $(\lambda \overline{a}, \overline{b})=\lambda(\overline{a}, \overline{b})$
7 $(\alpha \overline{a}+\beta \overline{b}, \gamma \overline{c}+\delta \overline{d})=\alpha \gamma(\overline{a}, \overline{c})+\alpha \delta(\overline{a}, \overline{d})+\beta \gamma(\overline{b}, \overline{c})+\beta \delta(\overline{b}, \overline{d})$
Если векторы $\overline{a}$ и $\overline{b}$ заданы своими координатами: $\overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right)$, $\overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right)$ , то их скалярное произведение вычисляется по формуле:
$(\overline{a}, \overline{b})=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}$
Определение
Скалярное произведение векторов, заданных своими координатами, равно сумме произведений соответствующих координат.
Пример
Задание. Найти скалярное произведение векторов $\overline{a}=(3 ;-1)$ и $\overline{b}=(-2 ; 7)$
Решение. Скалярное произведение
$\overline{a} \overline{b}=3 \cdot(-2)+(-1) \cdot 7=-6-7=-13$
Длина вектора
Длина вектора $\overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right)$, заданного своими координатами, находится по формуле:
$|\overline{a}|=\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}$
Определение
Длина (модуль) вектора, координаты которого известны, равен корню квадратному из суммы квадратов координат.
Пример
Задание. Найти длину вектора $\overline{a}=(-4 ; 3)$
Решение. Используя формулу, получаем:
$|\overline{a}|=\sqrt{(-4)^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}=5$
Угол между векторами
Угол между двумя векторами $\overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right)$, $\overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right)$:
$$\cos (\bar{a}, \bar{b})=\frac{(\bar{a} ; \bar{b})}{|\bar{a}| \cdot|\bar{b}|}=\frac{a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}} \cdot \sqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}$$Если угол между двумя векторами острый, то их скалярное произведение положительно; если угол между векторами тупой, то скалярное произведение этих векторов отрицательно. Скалярное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда эти векторы ортогональны.
Пример
Задание. Найти угол между векторами $\overline{a}=(1 ; \sqrt{3})$ и $\overline{b}=(1 ; 0)$
Решение. Косинус искомого угла
$$\cos (\bar{a}, \bar{b})=\frac{1 \cdot 1+\sqrt{3} \cdot 0}{\sqrt{1^{2}+(\sqrt{3})^{2}} \cdot \sqrt{1^{2}+0^{2}}}=\frac{1}{2}$$ $$(\bar{a}, \bar{b})=\arccos \frac{1}{2}=60^{\circ}$$Читать дальше: векторное произведение векторов.










