Натуральными числами называются числа, которые используются при счете или для указания порядкового номера предмета среди однородных предметов.
Содержание:
Определение натурального числа
Определение
Например. Натуральными будут такие числа: $2,37,145,1059,24411$
Натуральные числа, записанные в порядке возрастания, образуют числовой ряд. Он начинается с наименьшего натурально числа 1. Множество всех натуральных чисел обозначают $N=\{1,2,3, \dots n, \ldots\}$. Оно бесконечно, так как не существует наибольшего натурального числа. Если к любому натуральному числу прибавить единицу, то получаем натуральное число, следующее за данным числом.
Пример
Задание. Какие из следующих чисел являются натуральными?
$$-89 ; 7 ; \frac{4}{3} ; 34 ; 2 ; 11 ; 3,2 ; \sqrt[3]{129} ; \sqrt{5}$$
Ответ. $7 ; 34 ; 2 ; 11$
На множестве натуральных чисел вводится две основные арифметические операции - сложение и умножение. Для обозначения этих операций используются соответственно символы " + " и " • " (или " × ").
Сложение натуральных чисел
Каждой паре натуральных чисел $n$ и $m$ ставится в соответствие натуральное число $s$, называемое суммой. Сумма $s$ состоит из стольких единиц, сколько их содержится в числах $n$ и $m$. О числе $s$ говорят, что оно получено в результате сложения чисел $n$ и $m$, и пишут
$$n+m=s$$
Числа $n$ и $m$ называются при этом слагаемыми. Операция сложения натуральных чисел обладает следующими свойствами:
- Коммутативность: $n+m=m+n$
- Ассоциативность: $(n+m)+k=n+(m+k)$
Подробнее о сложении чисел читайте по ссылке.
Пример
Задание. Найти сумму чисел:
$13+9 \quad$ и $ \quad 27+(3+72)$
Решение. $13+9=22$
Для вычисления второй суммы, для упрощения вычислений, применим к ней вначале свойство ассоциативности сложения:
$$27+(3+72)=(27+3)+72=30+72=102$$
Ответ. $13+9=22 \quad;\quad 27+(3+72)=102$
Умножение натуральных чисел
Каждой упорядоченной паре натуральных чисел $n$ и $m$ ставится в соответствие натуральное число $r$, называемое их произведением. Произведение $r$ содержит стольких единиц, сколько их содержится в числе $n$, взятых столько раз, сколько единиц содержится в числе $m$. О числе $r$ говорят, что оно получено в результате умножения чисел $n$ и $m$, и пишут
$n \cdot m=r \quad $ или $ \quad n \times m=r$
Числа $n$ и $m$ называются множителями или сомножителями.
Операция умножения натуральных чисел обладает следующими свойствами:
- Коммутативность: $n \cdot m=m \cdot n$
- Ассоциативность: $(n \cdot m) \cdot k=n \cdot(m \cdot k)$
Подробнее о умножении чисел читайте по ссылке.
Пример
Задание. Найти произведение чисел:
12$\cdot 3 \quad $ и $ \quad 7 \cdot 25 \cdot 4$
Решение. По определению операции умножения:
$$12 \cdot 3=12+12+12=36$$
Ко второму произведению применим свойство ассоциативности умножения:
$$7 \cdot 25 \cdot 4=7 \cdot(25 \cdot 4)=7 \cdot 100=700$$
Ответ. $12 \cdot 3=36 \quad;\quad 7 \cdot 25 \cdot 4=700$
Операция сложения и умножения натуральных чисел связаны законом дистрибутивности умножения относительно сложения:
$$(n+m) \cdot k=n \cdot k+m \cdot k$$
Сумма и произведение любых двух натуральных чисел всегда есть число натуральное, поэтому множество всех натуральных чисел замкнуто относительно операций сложения и умножения.
Так же на множестве натуральных чисел можно ввести операции вычитания и деления, как операции обратные к операциям сложения и умножения соответственно. Но эти операции не будут однозначно определенны для любой пары натуральных чисел.
Свойство ассоциативности умножения натуральных чисел позволяет ввести понятие натуральной степени натурального числа: $n$-й степенью натурального числа $m$ называется натуральное число $k$, полученное в результате умножения числа $m$ самого на себя $n$ раз:
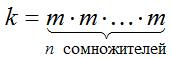
Для обозначения $n$-й степени числа $m$ обычно используется запись: $m^{n}$, в котором число $m$ называется \lt strong>основанием степени \lt /strong>, а число $n$ - показателем степени.
Пример
Задание. Найти значение выражения $2^{5}$
Решение. По определению натуральной степени натурального числа это выражение можно записать следующим образом
$$2^{5}=2 \cdot 2 \cdot 2 \cdot 2 \cdot 2=32$$
Ответ. $2^{5}=32$
Читать дальше: что такое рациональное число.










