Содержание:

Определение произведения чисел

Произведение $p$ чисел $a_{1}, a_{2}, \dots, a_{n}$ есть результат умножения этих чисел: $p=a_{1} \cdot a_{2} \cdot \ldots \cdot a_{n}$ . В частности, если умножаются два числа $a$ и $b$, то

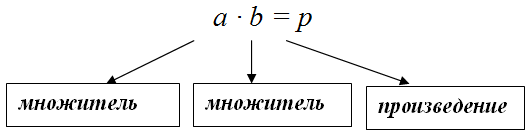
Пример

Задание. Найти произведение чисел:

1)  1.2$\cdot 3$   ;   2)  4$\cdot 5 \cdot 13$ 

Ответ.  

$1,2 \cdot 3=3,6$

$4 \cdot 5 \cdot 13=260$

Свойства произведения чисел

  1. Коммутативность: $n \cdot m=m \cdot n$

  2. Ассоциативность: $(n \cdot m) \cdot k=n \cdot(m \cdot k)$

    На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.

  3. Дистрибутивность: $(n+m) \cdot k=n \cdot k+m \cdot k$

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 465 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти произведение чисел удобным способом:

1)  5$\cdot 17 \cdot 2$   ;   2)  7$\cdot 2 \cdot 15 \cdot 5$ 

Решение. По свойства умножения имеем:

$$5 \cdot 17 \cdot 2=(5 \cdot 2) \cdot 17=10 \cdot 17=170$$

$$7 \cdot 2 \cdot 15 \cdot 5=(7 \cdot(2 \cdot 15)) \cdot 5=(7 \cdot 30) \cdot 5=210 \cdot 5=1050$$

Ответ.  

$5 \cdot 17 \cdot 2=170$

$7 \cdot 2 \cdot 15 \cdot 5=1050$

Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.

Пример

Задание. Найти произведение чисел

1)  156$\cdot 32$   ;   2)  $4,71 \cdot 3,1$ 

Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое, полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в столбик

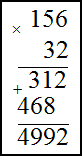
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором - один, значит, в ответе нужно отделить справа три знака:

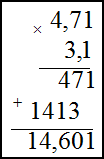
Ответ.  

$156 \cdot 32=4992$

$4,71 \cdot 3,1=14,601$

Десятичные дроби Умножение столбиком онлайн

Читать дальше: что такое простое число.