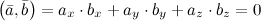Как найти вектор перпендикулярный вектору

Задание. Даны два вектора $\bar{a}=(2 ;-1)$ и $\bar{b}=(-3 ; m)$ . При каком значении $m$ эти векторы будут перпендикулярны?

Решение. Для того чтобы векторы $\bar{a}$ и $\bar{b}$ были перпендикулярны необходимо, чтобы их скалярное произведение было равно нулю, то есть выполнялось условие:

$$(\bar{a}, \bar{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y}=0$$

Подставим в это выражение координаты заданных векторов и из полученного равенства найдем $m$:

$$2 \cdot(-3)+(-1) \cdot m=0$$ $$-6-m=0$$ $$m=-6$$

Ответ. Векторы $\bar{a}$ и $\bar{b}$ будут перпендикулярны при $m=-6$

Задание. Заданы два вектора $\bar{a}=(3 ;-2 ; m)$ и $\bar{b}=(-1 ; m ; 1)$ . При каком значении $m$ эти векторы будут перпендикулярны?

Решение. Два вектора $\bar{a}$ и $\bar{b}$ будут перпендикулярны тогда, когда их скалярное произведение будет равняться нулю. И так как векторы заданны в пространстве, то должно выполнялось условие:

Подставим в него заданные координаты векторов, получим:

$$(\bar{a}, \bar{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y}+a_{z} \cdot b_{z}=0$$ $$3 \cdot(-1)+(-2) \cdot m+m \cdot 1=0$$ $$3-2 \cdot m+m=0$$

Из полученного уравнения найдем $m$:

$$3-m=0 \Rightarrow m=-3$$

Ответ. Векторы $\bar{a}$ и $\bar{b}$ будут перпендикулярны при $m=-3$