Определение

Корнем $n$-ой степени из комплексного числа $z$ называется такое комплексное число $w$, $n$-я степень которого равна $z$, то есть

$w^{n}=z$

Корень $n$-ой степени из комплексного числа $z$ обозначается символом $\sqrt[n]{z}$ и на множестве комплексных чисел имеет ровно $n$ значений.

Если комплексное число $z$ задано в тригонометрической форме: $z=|z|(\cos \phi+i \sin \phi)$, то все значения корня $n$-ой степени вычисляются по формуле Муавра (Абрахам де Муавр (1667 - 1754) - английский математик):

$\sqrt[n]{z}=\sqrt[n]{|z|}\left(\cos \frac{\phi+2 n k}{n}+i \sin \frac{\phi+2 n k}{n}\right), k=0,1,2, \ldots, n-1$

Геометрически все значения корня лежат на окружности радиуса $\sqrt[n]{|z|}$ с центром в начале координат и образуют правильный $n$-угольник.

Пример

Задание. Вычислить корень четвертой степени из $z=-1$

Решение. Запишем заданное число в тригонометрической форме, для этого вычислим модуль и аргумент:

$|z|=|-1|=\sqrt{(-1)^{2}+0^{2}}=1$

$\arg z=\arg (-1)=\operatorname{arctg} \frac{0}{-1}+\pi=\operatorname{arctg} 0+\pi=0+\pi=\pi$

То есть

$z=-1=1 \cdot(\cos \pi+i \sin \pi)=\cos \pi+i \sin \pi$

Тогда

$w_{k}=\sqrt[4]{z}=\sqrt[4]{-1}=\sqrt[4]{1} \cdot\left(\cos \frac{\pi+2 \pi k}{4}+i \sin \frac{\pi+2 \pi k}{4}\right)=$

$=\cos \frac{\pi+2 \pi k}{4}+i \sin \frac{\pi+2 \pi k}{4}, k=\overline{0 ; 3}$

Отсюда все значения корня:

$k=0 : w_{0}=\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2} i$

$k=1 : w_{1}=\cos \frac{\pi+2 \pi}{4}+i \sin \frac{\pi+2 \pi}{4}=\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}=$

$=-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2} i$

$k=2 : w_{2}=\cos \frac{\pi+4 \pi}{4}+i \sin \frac{\pi+4 \pi}{4}=\cos \frac{5 \pi}{4}+i \sin \frac{5 \pi}{4}=$

$=-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2} i$

$k=3 : w_{3}=\cos \frac{\pi+6 \pi}{4}+i \sin \frac{\pi+6 \pi}{4}=\cos \frac{7 \pi}{4}+i \sin \frac{7 \pi}{4}=$

$=\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2} i$

Покажем, что все значения корня лежат на окружности радиуса $\sqrt[4]{|z|}=\sqrt[4]{1}=1$ и образуют правильный четырехугольник, то есть квадрат (рис. 1):

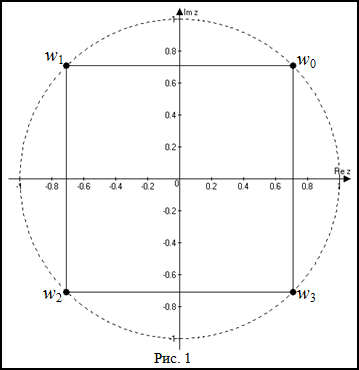
Ответ. $w_{0}=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2} i, w_{1}=-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2} i, w_{2}=-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2} i$

$w_{3}=\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2} i$ 

Читать дальше: формула Эйлера для комплексных чисел.

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 469 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!