Приведение дробей к общему знаменателю

Задание. Привести дроби  $\frac{3}{4}$  и  $\frac{5}{14}$  к общему знаменателю.

Решение. Каждая из дробей является несократимой, поэтому переходим к нахождению НОК знаменателей дробей - чисел 4 и 14. Для этого воспользуемся каноническими разложениями на простые множители:

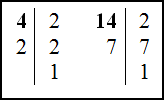
Получаем, что $4=2^{2}, 14=2 \cdot 7$ . Для нахождения НОК знаменателей из их канонических разложений выписываем все простые множители, которые входят хотя бы в одно из них. Из одинаковых простых множителей выбираем тот, который стоит в наибольшей степени. То есть в нашем случае имеем:

НОК (4, 14) $=2^{2} \cdot 7=28$

Вычисляем дополнительные множители к каждой из дробей, для этого найденный НОК делим соответственно на 4 и 14:

$28 : 4=7 ; 28 : 14=2$

Далее числитель и знаменатель первой дроби умножаем на дополнительный множитель, равный 7, а второй дроби - на 2, будем иметь:

$\frac{3}{4}=\frac{3 \cdot 7}{4 \cdot 7}=\frac{21}{28}$ и $\frac{5}{14}=\frac{5 \cdot 2}{14 \cdot 2}=\frac{10}{28}$

Полученные дроби  $\frac{21}{28}$  и  $\frac{10}{28}$  уже имеют общий знаменатель, равный 28.

Ответ. Дроби  $\frac{3}{4}$  и  $\frac{5}{14}$  с общим знаменателем: $\frac{3}{4}=\frac{21}{28}, \frac{5}{14}=\frac{10}{28}$