Сокращение дроби

Задание. Сократить дробь  $\frac{48}{88}$

Решение. Как видим, числитель и знаменатель заданной дроби являются четными числами, а поэтому и можно сократить на их общий делитель - 2:

$\frac{48}{88}=\frac{24}{44}$

Аналогично, общим делителем полученных числителя 24 и знаменателя 44 есть число 4, а поэтому производим дальнейшее сокращение на 4:

$\frac{48}{88}=\frac{24}{44}=\frac{6}{11}$

Полученные числа - 6 и 11 - уже являются взаимно простыми.

Итак, после сокращения окончательно имеем:

$\frac{48}{88}=\frac{6}{11}$

Ответ.   $\frac{48}{88}=\frac{6}{11}$

Задание. Сократить дробь $\frac{840}{3600}$

Решение. Вначале найдем НОД чисел 840 и 3600 двумя способами.

Первый способ: с помощью канонических разложений на простые множители. Запишем указанные канонические разложения:

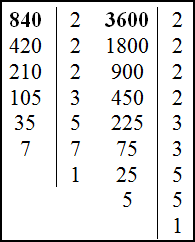
Таким образом, $840=2^{3} \cdot 3 \cdot 5 \cdot 7,3600=2^{4} \cdot 3^{2} \cdot 5^{2}$

Из полученных разложений выписываем одинаковые множители в наименьшей степени, что и определяет НОД:

НОД (840, 3600) $=2^{3} \cdot 3 \cdot 5=120$

Второй способ: с помощью алгоритма Евклида (Евклид или Эвклид (325 г. до н.э. - 265 г. до н.э.) - древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике).

НОД двух чисел равен последнему, неравному нулю остатку в алгоритме Евклида. Будем выполнять деление в столбик. Начнем с того, что знаменатель 3600 поделим на числитель 840 (большее число делится на меньшее):

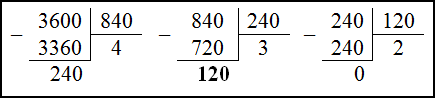
Итак, НОД (840, 3600) = 120

После того, как НОД найден, делим числитель и знаменатель дроби $\frac{840}{3600}$ на 120, в результате получим:

$\frac{840}{3600}=\frac{7}{30}$

Ответ.   $\frac{840}{3600}=\frac{7}{30}$