Примеры решения задач с логарифмами

Задание. Представить $\log _{5} 6$ в виде суммы логарифмов.

Решение. $\log _{5} 6=\log _{5}(2 \cdot 3)=\log _{5} 2+\log _{5} 3$

Задание. Упростить $\log _{5} 4+\log _{5} 3$

Решение. $\log _{5} 4+\log _{5} 3=\log _{5}(4 \cdot 3)=\log _{5} 12$

Задание. Известно, что $\log _{5} 2=a$, а $\log _{5} 3=b$. Выразить $\log _{5} \frac{2}{3}$ через $a$ и $b$.

Решение. $\log _{5} \frac{2}{3}=\log _{5} 2-\log _{5} 3=a-b$

Задание. Вычислить значение выражения $\log _{5} 10-\log _{5} 2$

Решение. $\log _{5} 10-\log _{5} 2=\log _{5} \frac{10}{2}=\log _{5} 5=1$

Задание. Вычислить $\log _{5} 10-\log _{5} 2=\log _{5} \frac{10}{2}=\log _{5} 5=1$

Решение.$\log _{2} \frac{1}{8}+\log _{5} 25=\log _{2} 2^{-3}+\log _{5} 5^{2}=-3 \cdot \log _{2} 2+2 \cdot \log _{5} 5=$

$= -3 + 2 = -1$

Задание. Упростить выражение $2 \log _{7} 4-\log _{7} 8$

Решение. $2 \log _{7} 4-\log _{7} 8=\log _{7} 4^{2}-\log _{7} 8=\log _{7} 16-\log _{7} 8=$

$=\log _{7} \frac{16}{8}=\log _{7} 2$

Задание. Вычислить $\log _{a} \sqrt{a b}$, если $\log _{a} b = 7$

Решение. $\log _{a} \sqrt{a b}=\frac{1}{2} \log _{a}(a b)=\frac{1}{2}\left(\log _{a} a+\log _{a} b\right)=$

$=\frac{1}{2}(1+7)=4$

Задание. Упростить выражение $\frac{1}{2} \log _{8} 16+\log _{8} 2$

Решение. $\frac{1}{2} \log _{8} 16+\log _{8} 2=\log _{8} \sqrt{16}+\log _{8} 2=$

$$=\log _{8} 4+\log _{8} 2=\log _{8}(4 \cdot 2)=\log _{8} 8=1$$

Задание. Разложить в ряд Маклорена функцию $f(x)=\ln \left(1+x^{2}\right)$

Решение. Сделаем замену $x^{2}=t$, тогда $f(x)=\ln (1+t)$. Используя приведенное выше разложение, получаем:

$$f(x)=\ln (1+t)=t-\frac{t^{2}}{2}+\frac{t^{3}}{3}-\ldots+(-1)^{n+1} \cdot \frac{t^{n}}{n}+\ldots,|t|<1$$

Делаем обратную замену, получаем:

$f(x)=\ln \left(1+x^{2}\right)=x^{2}-\frac{\left(x^{2}\right)^{2}}{2}+\frac{\left(x^{2}\right)^{3}}{3}-\ldots+(-1)^{n+1} \cdot \frac{\left(x^{2}\right)^{n}}{n}+\ldots,\left|x^{2}\right| \lt $ \lt p style="text-align:center;">или $$f(x)=\ln \left(1+x^{2}\right)=x^{2}-\frac{x^{4}}{2}+\frac{x^{6}}{3}-\ldots+(-1)^{n+1} \cdot \frac{x^{2 n}}{n}+\ldots,|x|<1$$

Задание. Прологарифмировать выражение

Решение. В левой и правой части допишем логарифм по основанию $\log _{a} x=\log _{a}(3 b c)$:

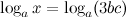
По свойствам логарифмов логарифм произведения, стоящий в правой части, представим как сумму логарифмов от каждого из сомножителей, то есть:

$\log _{a} x=\log _{a} 3+\log _{a} b+\log _{a} c$

Задание. Пропотенцировать выражение $\log _{a} x=5 \log _{a} c-\log _{a} d$

Решение. Используя свойства логарифмов, преобразуем правую часть данного выражения:

$$5 \log _{a} c-\log _{a} d=\log _{a} c^{5}-\log _{a} d=\log _{a} \frac{c^{5}}{d}$$ $$\log _{a} x=\log _{a} \frac{c^{5}}{d}$$ $$x=\frac{c^{5}}{d}$$

Задание. Решить уравнение $\log _{2}\left(x^{2}+4\right)=3$

Решение. ОДЗ: $x^{2}+4>0 \Rightarrow x \in R$

Замена: $x^{2}+4=t$, получаем уравнение $\log _{2} t=3$, решение которого

$t=2^{3}=8$

Делая обратную замену, получаем:

$x^{2}+4=8 \Rightarrow x^{2}-4=0 \Rightarrow(x-2)(x+2) \Rightarrow x_{1}=2, x_{2}=-2$

Ответ. $x_{1}=2, x_{2}=-2$

Задание. Найти решение уравнения $\log _{x}(x+2)=2$

Решение. ОДЗ:

$$\left\{\begin{array}{l} x+2>0, \\ x>0, \quad \Rightarrow \\ x \neq 1 \end{array} \quad\left\{\begin{array}{l} x>-2 \\ x>0, \quad \Rightarrow x \in(0 ; 1) \cup(1 ;+\infty) \\ x \neq 1 \end{array}\right.\right.$$

Замена: $x+2=t \Rightarrow \log _{x} t=2 \Rightarrow t=x^{2}$. Делая обратную замену, приходим к уравнению

$$x^{2}=x+2 \Rightarrow x^{2}-x-2=0 \Rightarrow x_{1}=2, x_{2}=-1$$

Второй корень не принадлежит ОДЗ, а значит решение $x=2$

Ответ. $x=2$

Задание. Решить уравнение $\ln (x+1)=\ln (2 x-3)$

Решение. Находим ОДЗ:

$$\left\{\begin{array}{l} x+1>0 \\ 2 x-3>0 \end{array} \Rightarrow\left\{\begin{array}{l} x>-1 \\ 2 x>3 \end{array} \Rightarrow\left\{\begin{array}{l} x>-1 \\ x>\frac{3}{2} \end{array} \Rightarrow\left(\frac{3}{2} ;+\infty\right)\right.\right.\right.$$

Решаем уравнение $x+1=2 x-3: x=4 \in$ ОДЗ.

Итак, решением исходного логарифмического уравнения также является это значение.

Ответ. $x=4$

Задание. Решить неравенство $\log _{0,5}(x-1)>-1$

Решение. ОДЗ:

$$x-1>0 \Rightarrow x>1 \Rightarrow x \in(1 ;+\infty)$$

Учитывая выше написанное, получаем, что заданное логарифмическое неравенство равносильно неравенству:

$x-1 <0,5^{-1}$   или   $x-1<2 \Rightarrow x<3$

В пересечении с ОДЗ получаем, что $x \in(1 ; 3)$

Ответ. $x \in(1 ; 3)$

Задание. Решить неравенство $\log _{5} 5>\log _{5} x$

Решение. Данное неравенство равносильно системе:

$$\left\{\begin{array}{l} 5>x, \\ x>0 \end{array} \Rightarrow\left\{\begin{array}{l} x0 \end{array} \Rightarrow x \in(0 ; 5)\right.\right.$$

Ответ. $x \in(0 ; 5)$