Тригонометрические формулы

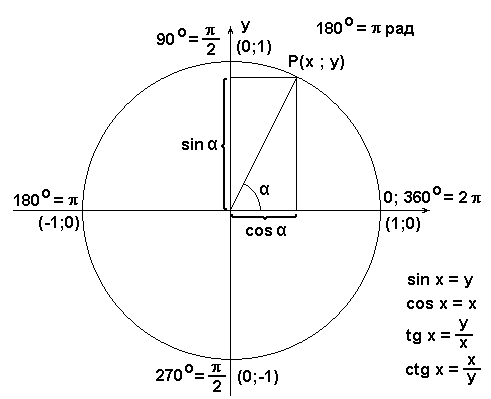
Формулы, связывающие функции одного аргумента (угла) (11 шт)

$$ \sin ^{2}(\alpha)+\cos ^{2}(\alpha)=1 \quad \operatorname{tg}(\alpha) \cdot \operatorname{ctg}(\alpha)=1 $$
$$ 1+\operatorname{tg}^{2}(\alpha)=\frac{1}{\cos ^{2}(\alpha)} \quad 1+\operatorname{ctg}^{2}(\alpha)=\frac{1}{\sin ^{2}(\alpha)} $$
$$ \sin (\alpha)=\sqrt{1-\cos ^{2}(\alpha)}=-\sqrt{1-\cos ^{2}(\alpha)} $$
$$ \cos (\alpha)=\sqrt{1-\sin ^{2}(\alpha)}=-\sqrt{1-\sin ^{2}(\alpha)} $$
$$ \operatorname{cosec}(\alpha)=\frac{1}{\sin (\alpha)} \quad \sec (\alpha)=\frac{1}{\cos (\alpha)} $$
$$ \sec ^{2}(\alpha)=1+\operatorname{tg}^{2}(\alpha) \quad \operatorname{cosec}^{2}(\alpha)=1+\operatorname{ctg}^{2}(\alpha) $$
$$ \operatorname{tg}(\alpha)=\frac{\sin (\alpha)}{\cos (\alpha)}=\frac{1}{\operatorname{ctg}(\alpha)} $$

Формулы суммы и разности (16 шт)

$$ \sin (\alpha+\beta)=\sin (\alpha) \cdot \cos (\beta)+\cos (\alpha) \cdot \sin (\beta) $$
$$ \sin (\alpha-\beta)=\sin (\alpha) \cdot \cos (\beta)-\cos (\alpha) \cdot \sin (\beta) $$
$$ \cos (\alpha+\beta)=\cos (\alpha) \cdot \cos (\beta)-\sin (\alpha) \cdot \sin (\beta) $$
$$ \cos (\alpha-\beta)=\cos (\alpha) \cdot \cos (\beta)+\sin (\alpha) \cdot \sin (\beta) $$
$$ \operatorname{tg}(\alpha+\beta)=\frac{\operatorname{tg}(\alpha)+\operatorname{tg}(\beta)}{1-\operatorname{tg}(\alpha) \cdot \operatorname{tg}(\beta)} \operatorname{tg}(\alpha-\beta)=\frac{\operatorname{tg}(\alpha)-\operatorname{tg}(\beta)}{1+\operatorname{tg}(\alpha) \cdot \operatorname{tg}(\beta)} $$
$$ \operatorname{ctg}(\alpha+\beta)=\frac{\operatorname{ctg}(\alpha) \cdot \operatorname{ctg}(\beta)-1}{\operatorname{ctg}(\alpha)-\operatorname{ctg}(\beta)} \operatorname{ctg}(\alpha+\beta)=\frac{\operatorname{ctg}(\alpha) \cdot \operatorname{ctg}(\beta)-1}{\operatorname{ctg}(\alpha)-\operatorname{ctg}(\beta)} $$
$$ \sin (\alpha)+\sin (\beta)=2 \cdot \sin \left(\frac{\alpha+\beta}{2}\right) \cdot \cos \left(\frac{\alpha-\beta}{2}\right) $$
$$ \sin (\alpha)-\sin (\beta)=2 \cdot \cos \left(\frac{\alpha+\beta}{2}\right) \cdot \sin \left(\frac{\alpha-\beta}{2}\right) $$
$$ \cos (\alpha)+\cos (\beta)=2 \cdot \cos \left(\frac{\alpha+\beta}{2}\right) \cdot \cos \left(\frac{\alpha-\beta}{2}\right) $$
$$ \cos (\alpha)-\cos (\beta)=-2 \cdot \sin \left(\frac{\alpha+\beta}{2}\right) \cdot \sin \left(\frac{\alpha-\beta}{2}\right) $$
$$ \operatorname{tg}(\alpha)+\operatorname{tg}(\beta)=\frac{\sin (\alpha+\beta)}{\cos (\alpha) \cdot \cos (\beta)} \operatorname{tg}(\alpha)-\operatorname{tg}(\beta)=\frac{\sin (\alpha-\beta)}{\cos (\alpha) \cdot \cos (\beta)} $$
$$ \operatorname{ctg}(\alpha)+\operatorname{ctg}(\beta)=\frac{\sin (\beta+\alpha)}{\sin (\alpha) \cdot \sin (\beta)} \quad \operatorname{ctg}(\alpha)-\operatorname{ctg}(\beta)=\frac{\sin (\beta-\alpha)}{\sin (\alpha) \cdot \sin (\beta)} $$

Формулы понижения степени (10 шт)

$$ \sin ^{2}(\alpha)=\frac{1-\cos (2 \alpha)}{2} \quad \cos ^{2}(\alpha)=\frac{1+\cos (2 \alpha)}{2} $$
$$ \operatorname{tg}^{2}(\alpha)=\frac{1-\cos (2 \alpha)}{1+\cos (2 \alpha)} \quad \operatorname{ctg}^{2}(\alpha)=\frac{1+\cos (2 \alpha)}{1-\cos (2 \alpha)} $$
$$ \cos ^{3}(\alpha)=\frac{1}{4}(3 \cdot \cos (\alpha)+\cos (3 \alpha)) $$
$$ \sin ^{3}(\alpha)=\frac{1}{4}(3 \cdot \sin (\alpha)-\sin (3 \alpha)) $$
$$ \cos ^{4}(\alpha)-\sin ^{4}(\alpha)=\cos (2 \alpha) $$
$$ \cos ^{4}(\alpha)+\sin ^{4}(\alpha)=1-\frac{\sin ^{2}(2 \alpha)}{2} $$
$$ \cos ^{6}(\alpha)+\sin ^{6}(\alpha)=1-\frac{3}{4} \sin ^{2}(2 \alpha) $$
$$ \cos ^{6}(\alpha)-\sin ^{6}(\alpha)=\cos (2 \alpha) \cdot\left[1-\frac{1}{4} \sin ^{2}(2 \alpha)\right] $$

Формулы для функций кратных аргументов (11 шт)

$$ \sin (2 \alpha)=2 \cdot \sin (\alpha) \cdot \cos (\alpha) $$
$$ \cos (2 \alpha)=\cos ^{2}(\alpha)-\sin ^{2}(\alpha)=2 \cdot \cos ^{2}(\alpha)-1=1-2 \cdot \sin ^{2}(\alpha) $$
$$ \operatorname{tg}(2 \alpha)=\frac{2 \cdot \operatorname{tg}(\alpha)}{1-\operatorname{tg}^{2}(\alpha)} \quad \operatorname{ctg}(2 \alpha)=\frac{\operatorname{ctg}^{2}(\alpha)-1}{2 \cdot \operatorname{ctg}(\alpha)} $$
$$ \sin (3 \alpha)=3 \cdot \sin (\alpha)-4 \cdot \sin ^{3}(\alpha) $$
$$ \cos (3 \cdot \alpha)=4 \cdot \cos ^{3}(\alpha)-3 \cdot \cos (\alpha) $$
$$ \operatorname{tg}(3 \alpha)=\frac{3 \cdot \operatorname{tg}(\alpha)-\operatorname{tg}^{3}(\alpha)}{1-3 \cdot \operatorname{tg}^{2}(\alpha)}=\operatorname{tg}(\alpha) \cdot \operatorname{tg}\left(\frac{\pi}{3}+\alpha\right) \cdot \operatorname{tg}\left(\frac{\pi}{3}-\alpha\right) $$
$$ \operatorname{ctg}(3 \cdot \alpha)=\frac{3 \cdot \operatorname{ctg}(\alpha)-\operatorname{ctg}^{3}(\alpha)}{1-3 \cdot \operatorname{ctg}^{2}(\alpha)} $$

Формулы произведения функций (6 шт)

$$ \sin (\alpha) \cdot \sin (\beta)=\frac{1}{2}(\cos (\alpha-\beta)-\cos (\alpha+\beta)) $$
$$ \cos (\alpha) \cdot \cos (\beta)=\frac{1}{2}(\cos (\alpha-\beta)+\cos (\alpha+\beta)) $$
$$ \sin (\alpha) \cdot \cos (\beta)=\frac{1}{2}(\sin (\alpha-\beta)+\sin (\alpha+\beta)) $$
$$ \operatorname{tg}(\alpha) \cdot \operatorname{tg}(\beta)=\frac{\operatorname{tg}(\alpha)+\operatorname{tg}(\beta)}{\operatorname{ctg}(\alpha)+\operatorname{ctg}(\beta)} \quad \operatorname{ctg}(\alpha) \cdot \operatorname{ctg}(\beta)=\frac{\operatorname{ctg}(\alpha)+\operatorname{ctg}(\beta)}{\operatorname{tg}(\alpha)+\operatorname{tg}(\beta)} $$
$$ \operatorname{ctg}(\alpha) \cdot \operatorname{tg}(\beta)=\frac{\operatorname{ctg}(\alpha)+\operatorname{tg}(\beta)}{\operatorname{tg}(\alpha)+\operatorname{ctg}(\beta)} $$

Формулы, связывающие все тригонометрические функции с тангенсом половинного угла (3 шт)

$$ \sin (\alpha)=\frac{2 \cdot \operatorname{tg}\left(\frac{\alpha}{2}\right)}{1+\operatorname{tg}^{2}\left(\frac{\alpha}{2}\right)} \quad \cos (\alpha)=\frac{1-\operatorname{tg}^{2}\left(\frac{\alpha}{2}\right)}{1+\operatorname{tg}^{2}\left(\frac{\alpha}{2}\right)} \quad \operatorname{tg}(\alpha)=\frac{2 \cdot \operatorname{tg}\left(\frac{\alpha}{2}\right)}{1-\operatorname{tg}^{2}\left(\frac{\alpha}{2}\right)} $$