Что такое правильный треугольник

Задание. Найти, чему равна высота равностороннего треугольника со стороною $a = 4$ см.

Решение. Сделаем рисунок (рис. 2).

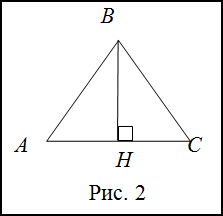
Высота в равностороннем треугольнике является так же и медианой, поэтому:

$A H=H C=\frac{1}{2} A C=2$

Далее, рассмотрим $\Delta B H C$, этот треугольник прямоугольный. По теореме Пифагора:

$$B H=\sqrt{B C^{2}-H C^{2}}$$

то есть

$B H=\sqrt{4^{2}-2^{2}}=\sqrt{16-4}=\sqrt{12}=2 \sqrt{3}$ (см)

Ответ. $B H=2 \sqrt{3}$ см

Задание. Найти сторону равностороннего треугольника, если его высота равна $3 \sqrt{3}$ дм.

Решение. Сделаем рисунок (рис. 2).

Рассмотрим $\Delta B C H$, он прямоугольный. Обозначим $BC = a$, тогда $H C=\frac{a}{2}$ . Запишем теорему Пифагора для рассматриваемого треугольника:

$$B C^{2}=H C^{2}+B H^{2}$$

Используя введенные обозначения и исходные данные, получим

$$a^{2}=\left(\frac{a}{2}\right)^{2}+(3 \sqrt{3})^{2}$$

Решим полученное уравнение относительно $a$:

$$ \begin{array}{c} a^{2}=\frac{a^{2}}{4}+27 \\ a^{2}-\frac{a^{2}}{4}=27 \\ \frac{3 a^{2}}{4}=27 \\ a^{2}=\frac{27 \cdot 4}{3}=36 \\ a=\sqrt{36}=6 \\ a=6 \end{array} $$

Ответ. $a = 6$ дм.

Задание. Дан равносторонний треугольник $ABC$, со стороной $a=6 \sqrt{3}$ см. Найти радиусы вписанной и описанной окружностей.

Решение. Сделаем рисунок (рис. 3).

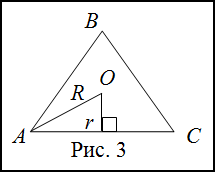
Радиус $r$ вписанной и радиус $R$ описанной окружностей равностороннего треугольника связаны с его длиной $a$ следующими соотношениями:

$$r=\frac{\sqrt{3}}{6} a, \quad R=\frac{\sqrt{3}}{3} a$$

Подставляя значение $a=6 \sqrt{3}$, получим:

$r=\frac{\sqrt{3} \cdot 6 \sqrt{3}}{6}=3(\mathrm{~cm}) \quad, \quad R=\frac{\sqrt{3} \cdot 6 \sqrt{3}}{3}=6$ (см)

Ответ. $r = 3$ см , $R = 6$ см