Содержание:

Определение медианы треугольника

Определение

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

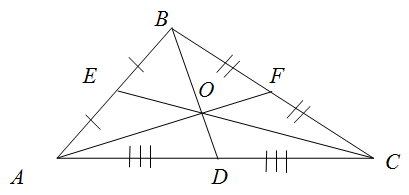
В каждом треугольнике существует три различные медианы (на рисунке отрезки $A F, B D, C E$ ), которые пересекаются в одной точке, лежащей внутри треугольника. Точка пересечения является центром масс данного треугольника.

Свойства медиан треугольника

  1. Медианы треугольника точкой их пересечения (на рисунке точка $O$ ) делятся в отношении $2 : 1$, считая от вершин треугольника.
  2. Медиана делит треугольник на два равновеликих треугольника (два треугольника равновелики, если их площади равны).
  3. Три медианы треугольника делят треугольник на шесть равновеликих треугольников (на рисунке это треугольники $\Delta A O E, \Delta B O E, \Delta B O F, \Delta C O F, \Delta C O D, \Delta A O D$).

  4. Медиана треугольника $m_a$ , проведенная к стороне $a$, выражается через стороны треугольника по формуле

    $$m_{a}=\frac{1}{2} \sqrt{2 b^{2}+2 c^{2}-a^{2}}$$

Примеры решения задач

Пример

Задание. В треугольнике $\Delta A B C$ медианы $A F$ и $B D$ пересекаются в точке $O$, $A F=6$ см. Найти длину отрезка $OF.

Решение. По свойству медиан треугольника точка их пересечения делит медиану в соотношении $2 : 1$, считая от вершин треугольника.

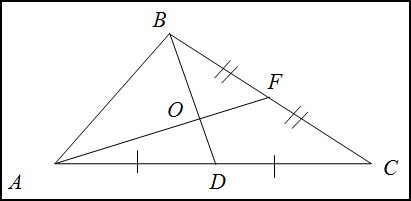
Таким образом, $A O : O F=2 : 1$. Положим $O F=x$ см, тогда $A O=2 x$ см. Так как $A F=A O+O F$, приходим к уравнению

$6=2 x+x$

$6=3 x$

$x=2$

Ответ. $O F=2$ см


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 445 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. В треугольнике $ABC$ $AB=\sqrt{3}$ см, $AC=2$ см и $BC=1$ см. Найти длину медианы $BM$.

Решение. Так как медиана треугольника $m_{a}$ , проведенная к стороне $a$, выражается через стороны треугольника по формуле

$$m_{a}=\frac{1}{2} \sqrt{2 b^{2}+2 c^{2}-a^{2}}$$

то искомая медиана $BM$ равна:

$$B M=\frac{1}{2} \sqrt{2 A B^{2}+2 B C^{2}-A C^{2}}$$

Подставляя исходные данные, получим:

$B M=\frac{1}{2} \sqrt{2 \cdot(\sqrt{3})^{2}+2 \cdot 1^{2}-2^{2}}$

$B M=\frac{1}{2} \sqrt{2 \cdot 3+2-4}$

$B M=\frac{1}{2} \cdot \sqrt{4}$

$B M=1$ (см)

Ответ. $B M=1$ см

Читать дальше: что такое высота треугольника.