Биссектрисой треугольника называется отрезок, который соединяет вершину с противоположной стороной и делит соответствующий угол пополам.
Содержание:
Определение биссектрисы треугольника
Определение
Каждый треугольник имеет три биссектрисы.
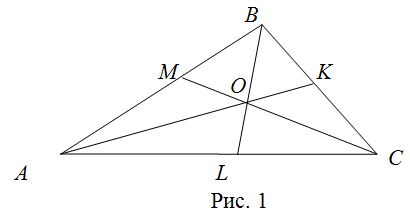
На рисунке 1 в треугольнике $A B C : M C$ - биссектриса угла $C, K A$ - биссектриса угла $A, B L$ - биссектриса угла $B$. Биссектрисы пересекаются в одной точке (на рисунке 1 точка $O$ ), которая лежит в середине треугольника и называется инцентром.
Свойство биссектрисы треугольника
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные к прилегающим сторонам:
$$\frac{A B}{B C}=\frac{L A}{L C}$$
Примеры решения задач
Пример
Задание. В треугольнике $\triangle A B C : B L$ - биссектриса, сторона $A B=5$ см, $B C=4$ см, отрезок $L C=2$ см. Найти длину отрезка $A L$.
Решение. По свойству биссектрисы
$$\frac{A B}{B C}=\frac{A L}{L C}$$
Подставляя в это равенство исходные данные, получим
$\frac{5}{4}=\frac{A L}{2} \Rightarrow A L=\frac{5 \cdot 2}{4} \Rightarrow A L=2,5$ (см)
Ответ. $A L=2,5$ см
Пример
Задание. В треугольнике $\Delta A B C : B L$ и $KA$ - биссектрисы, при пересечении которых образуется угол $115^{\circ}$. Найти угол $\angle C$.
Решение. Так как $B L$ и $K A$ - биссектрисы углов $\angle A$ и $\angle B$, то
$$\angle K A L=\frac{1}{2} \angle A, \quad \angle A B L=\frac{1}{2} \angle B$$
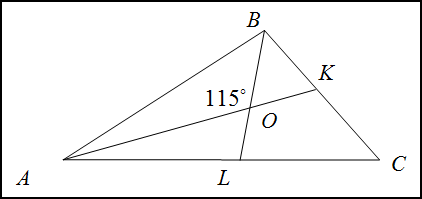
Из $\triangle A B O$ по теореме о сумме углов треугольника
$$\angle K A L+\angle A B L+\angle A B O=180^{\circ}$$
или
$$\frac{1}{2} \angle A+\frac{1}{2} \angle B+115^{\circ}=180^{\circ}$$
Откуда
$$\frac{1}{2} \angle A+\frac{1}{2} \angle B=180^{\circ}-115^{\circ}$$
$$\frac{1}{2}(\angle A+\angle B)=65^{\circ}$$
$$\angle A+\angle B=65^{\circ} \cdot 2$$
$$\angle A+\angle B=130^{\circ}$$
Далее из треугольника $A B C$ по теореме о сумме углов треугольника:
$$\angle A+\angle B+\angle C=180^{\circ}$$
Выразим из этого равенства угол $C$,
$$\angle C=180^{\circ}-(\angle A+\angle B)$$
подставляя уже имеющиеся значения для суммы углов, получим
$$\angle C=180^{\circ}-130^{\circ}=60^{\circ}$$
Ответ. $\angle C=60^{\circ}$
Читать дальше: что такое вершина треугольника.










