Что такое остроугольный треугольник

Задание. Определить какой из треугольников на рисунке 1 является остроугольным.

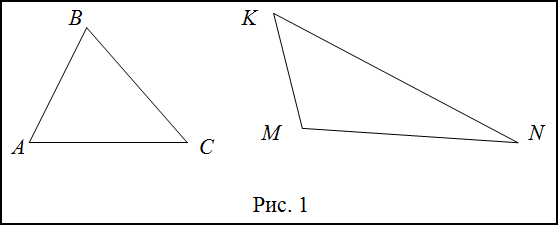
Решение. Сравним углы треугольников $ABC$ и $KMN$ с прямым углом. Для этого в каждой из вершин треугольника построим прямой угол.

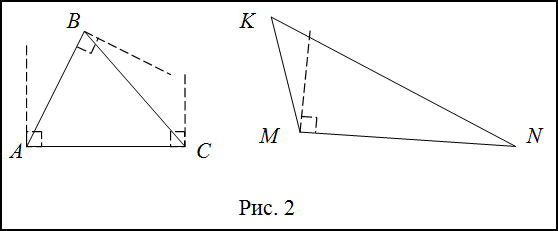
В треугольнике $ABC$ как видно, все углы меньше прямого, следовательно, он остроугольный. В треугольнике $KMN$ $\angle M$ больше, чем прямой угол, поэтому этот треугольник тупоугольный.

Ответ. $\Delta A B C$ - остроугольный.

Задание. В треугольниках $ABC$ и $KMN$ известны два угла: $\angle A=52^{\circ}$, $\angle C=42^{\circ}$, $\angle M=32^{\circ}$, $\angle N=22^{\circ}$. Определить есть ли среди них остроугольный треугольник.

Решение. Найдем недостающие углы в треугольниках, для этого воспользуемся теоремой про сумму углов треугольника.

В треугольнике $ABC$:

$$\angle B=180^{\circ}-\angle A-\angle C=180^{\circ}-52^{\circ}-42^{\circ}=86^{\circ}$$

Таким образом, в треугольнике $ABC$ все углы меньше $90^{\circ}$, значит он остроугольный.

В треугольнике $KMN$:

$$\angle K=180^{\circ}-\angle M-\angle N=180^{\circ}-32^{\circ}-22^{\circ}=126^{\circ}$$

Таким образом, в треугольнике $KMN$ угол $\angle K$ больше $90^{\circ}$, значит он тупоугольный.

Ответ. $ABC$ - остроугольный.