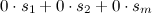Задание. Показать, что система строк $\left\{s_{1}=\left(\begin{array}{cc}
1 & 0
\end{array}\right), s_{2}=\left(\begin{array}{cc}
1 & 1
\end{array}\right)\right\}$ является ЛНЗ.
Решение. Составим ЛК заданных строк:
$$\lambda_{1} s_{1}+\lambda_{2} s_{2}=\left(\begin{array}{cc}
\lambda_{1} & 0
\end{array}\right)+\left(\begin{array}{cc}
\lambda_{2} & \lambda_{2}
\end{array}\right)=\left(\begin{array}{c}
\lambda_{1}+\lambda_{2} & \lambda_{2}
\end{array}\right)=$$
$$=\left(\begin{array}{ll}
0 & 0
\end{array}\right) \Longrightarrow\left\{\begin{array}{l}
\lambda_{1}+\lambda_{2}=0 \\
\lambda_{2}=0
\end{array} \Rightarrow\left\{\begin{array}{l}
\lambda_{1}=0 \\
\lambda_{2}=0
\end{array}\right.\right.$$
То есть ЛК данных строк равна нулевой строке, только если коэффициенты равны нулю одновременно.