Содержание:

Определение

Матрицей размера $m \times n$ называется прямоугольная таблица, содержащая $m \cdot n$ чисел, состоящая из $m$ строк и $n$ столбцов.

Обозначение

Таблица берется либо в круглые скобки, либо окружается двумя параллельными вертикальными прямыми.

Пример

$A=\left( \begin{array}{rrr}{1} & {4} & {0} \\ {-1} & {3} & {7}\end{array}\right)=\left|\left| \begin{array}{rrr}{1} & {4} & {0} \\ {-1} & {3} & {7}\end{array}\right|\right|$

Если матрица содержит $m$ строк и $n$ столбцов, то матрица называется матрицей размера $m \times n$ или $m \times n$-матрицей. Размер матрицы указывается справа внизу возле ее имени, либо таблицы с обозначением элементов.


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 467 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

$A_{2 \times 3}=\left( \begin{array}{rrr}{1} & {4} & {0} \\ {-1} & {3} & {7}\end{array}\right)_{2 \times 3}=\left|\left|\left.\begin{array}{rrr}{1} & {4} & {0} \\ {-1} & {3} & {7}\end{array}\right|\right|_{2 \times 3}\right.$

Элементы матрицы

Элементы матрицы $A$ обозначаются $a_{ij}$, где $i$ - номер строки, в которой находится элемент, а $j$ - номер столбца.

Пример

Задание. Чему равен элемент $a_{23}$ матрицы $A=\left( \begin{array}{rrr}{1} & {4} & {0} \\ {-1} & {3} & {7}\end{array}\right)$ ?

Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:

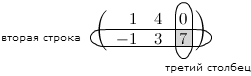
Таким образом, $a_{23} = 7$.

Ответ. $a_{23} = 7$

Определение

Строка матрицы называется нулевой, если все ее элементы равны нулю. Если хотя бы один из элементов строки не равен нулю, то строка называется ненулевой.

Замечание. Аналогичное определение и для нулевого и ненулевого столбцов матрицы.

Пример

В матрице $A=\left( \begin{array}{rr}{0} & {0} \\ {-1} & {0}\end{array}\right)$ первая строка является нулевой (любой элемент этой строки равен нулю); вторая строка ненулевая, так как элемент $a_{21}=-1 \neq 0$.

Диагонали

Определение

Главной диагональю матрицы называется диагональ, проведённая из левого верхнего угла матрицы в правый нижний.

Побочной диагональю матрицы называется диагональ, проведённая из левого нижнего угла матрицы в правый верхний.

Пример

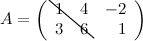Главная диагональ матрицы : 1 и 6 - элементы главной диагонали.

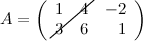Побочная диагональ матрицы : 3 и 4 - элементы побочной диагонали.

Для матрицы 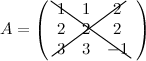элементы 1, 2, -1 образуют главную диагональ; а элементы 3, 2, 2 - побочную.

Читать дальше: виды матриц.