Примеры решения СЛАУ

Задание. Проверить, является ли набор ${0,3}$ решением системы $\left\{\begin{array}{l} 3 x-2 y=-6 \\ 5 x+y=3 \end{array}\right.$

Решение. Подставляем в каждое из уравнений системы $x=0$ и $y=3$ :

$$3 x-2 y=-6 \Rightarrow 3 \cdot 0-2 \cdot 3=-6 \Rightarrow-6=-6$$ $$5 x+y=3 \Rightarrow 5 \cdot 0+3=3 \Rightarrow 3=3$$

Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является решением указанной СЛАУ.

Ответ. Набор ${0,3}$ является решением системы $\left\{\begin{array}{l} 3 x-2 y=-6 \\ 5 x+y=3 \end{array}\right.$

Задание. Систему $\left\{\begin{array}{l} x-y+z-4 t=0 \\ 5 x+y+t=-11 \end{array}\right.$ записать в матричной форме и выписать все матрицы, которые ей соответствуют.

Решение. Заданную СЛАУ записываем в матричной форме $A \cdot X=B$ , где матрица системы:

$$A=\left(\begin{array}{rrrr} 1 & -1 & 1 & -4 \\ 5 & 1 & 0 & 1 \end{array}\right)$$

вектор-столбец неизвестных:

$$A=\left(\begin{array}{rrrr} 1 & -1 & 1 & -4 \\ 5 & 1 & 0 & 1 \end{array}\right)$$

вектор-столбец свободных коэффициентов:

$$B=\left(\begin{array}{c} 0 \\ -11 \end{array}\right)$$

то есть, запись СЛАУ в матричной форме:

$$\left(\begin{array}{rrrr} 1 & -1 & 1 & -4 \\ 5 & 1 & 0 & 1 \end{array}\right)\left(\begin{array}{l} x \\ y \\ z \\ t \end{array}\right)=\left(\begin{array}{r} 0 \\ -11 \end{array}\right)$$

Задание. Записать матрицу и расширенную матрицу системы $\left\{\begin{array}{l} 2 x_{1}+x_{2}-x_{3}=4 \\ x_{1}-x_{2}=5 \end{array}\right.$

Решение. Матрица системы $A=\left(\begin{array}{rrr} 2 & 1 & -1 \\ 1 & -1 & 0 \end{array}\right)$ , тогда расширенная матрица $\tilde{A}=(A \mid B)=\left(\begin{array}{rrr|r} 2 & 1 & -1 & 4 \\ 1 & -1 & 0 & 5 \end{array}\right)$

Задание. При каких значениях $\lambda$ система $\left\{\begin{array}{l} 2 x_{1}-x_{2}+x_{3}+x_{4}=1 \\ x_{1}+2 x_{2}-x_{3}+x_{4}=2 \\ x_{1}+7 x_{2}-4 x_{3}+2 x_{4}=\lambda \end{array}\right.$ будет совместной?

Решение. Ранг матрицы равен количеству ненулевых строк после приведения этой матрицы к ступенчатому виду. Поэтому записываем расширенную матрицу системы $\tilde{A}$ (слева от вертикальной черты находится матрица системы $A$ ):

$$\tilde{A}=\left(\begin{array}{rrrr|r} 2 & -1 & 1 & 1 & 1 \\ 1 & 2 & -1 & 1 & 2 \\ 1 & 7 & -4 & 2 & \lambda \end{array}\right)$$

и с помощью элементарных преобразований приводим ее к ступенчатому виду. Для этого вначале от второй строки отнимаем две вторых строки, а от третьей вторую, в результате получаем:

$$\tilde{A} \sim\left(\begin{array}{rrrr|r} 0 & -5 & 3 & -1 & -3 \\ 1 & 2 & -1 & 1 & 2 \\ 0 & 5 & -3 & 1 & \lambda-2 \end{array}\right)_{+I} \sim$$

Третью строку складываем с первой:

$$\tilde{A} \sim\left(\begin{array}{rrrr|r} 0 & -5 & 3 & -1 & -3 \\ 1 & 2 & -1 & 1 & 2 \\ 0 & 0 & 0 & 0 & \lambda-5 \end{array}\right)$$

и меняем первую и вторую строки матрицы местами

$$\tilde{A} \sim\left(\begin{array}{rrrr|r} 1 & 2 & -1 & 1 & 2 \\ 0 & -5 & 3 & -1 & -3 \\ 0 & 0 & 0 & 0 & \lambda-5 \end{array}\right)$$

Матрица приведена к ступенчатому виду. Получаем, что $rangA=2$ , $\operatorname{rang} \tilde{A}=\left\{\begin{array}{l} 2, \lambda=5 \\ 3, \lambda \neq 5 \end{array}\right.$ . Таким образом, при $\lambda=5$ система совместна, а при $\lambda \neq 5$ - несовместна.

Задание. Найти решение СЛАУ $\left\{\begin{array}{l}5 x_{1}+2 x_{2}=7 \\ 2 x_{1}+x_{2}=9\end{array}\right.$ матричным методом.

Решение. Выпишем матрицу системы $\left\{\begin{array}{l} 5 x_{1}+2 x_{2}=7 \\ 2 x_{1}+x_{2}=9 \end{array}\right.$ и матрицу правых частей $B=\left(\begin{array}{l} 7 \\ 9 \end{array}\right)$ . Найдем обратную матрицу для матрицы системы. Для матрицы второго порядка обратную можно находить по следующему алгоритму: 1) матрица должна быть невырождена, то есть ее определитель не должен равняться нулю: $|A|=1$ ; 2) элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный и делим полученные элементы на определитель матрицы. Итак, получаем, что

$$A^{-1}=\left(\begin{array}{rr} 1 & -2 \\ -2 & 5 \end{array}\right)$$

Тогда

$$X=\left(\begin{array}{l} x_{1} \\ x_{2} \end{array}\right)=A^{-1} B=\left(\begin{array}{rr} 1 & -2 \\ -2 & 5 \end{array}\right) \cdot\left(\begin{array}{l} 7 \\ 9 \end{array}\right)=$$ $$=\left(\begin{array}{r} -11 \\ 31 \end{array}\right) \Rightarrow\left(\begin{array}{l} x_{1} \\ x_{2} \end{array}\right)=\left(\begin{array}{r} -11 \\ 31 \end{array}\right)$$

Две матрицы одного размера равны, если равны их соответствующие элементы, то есть в итоге имеем, что $x_{1}=-11$, $x_{2}=31$

Ответ. $x_{1}=-11$, $x_{2}=31$

Задание. Решить с помощью обратной матрицы систему $\left\{\begin{array}{l} 2 x_{1}+x_{2}+x_{3}=2 \\ x_{1}-x_{2}=-2 \\ 3 x_{1}-x_{2}+2 x_{3}=2 \end{array}\right.$

Решение. Запишем данную систему в матричной форме:

$AX=B$,

где $A=\left(\begin{array}{rrr} 2 & 1 & 1 \\ 1 & -1 & 0 \\ 3 & -1 & 2 \end{array}\right)$ - матрица системы, $X=\left(\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}\right)$ - столбец неизвестных, $B=\left(\begin{array}{r} 2 \\ -2 \\ 2 \end{array}\right)$ - столбец правых частей. Тогда

$$X=A^-1B$$

Найдем обратную матрицу $A^-1$ к матрице $A$ с помощью союзной матрицы:

$$A^{-1}=\frac{1}{\Delta} \cdot \widetilde{A}^{T}$$

Здесь $\Delta=|A|$ - определитель матрицы $A$ ; матрица $\tilde{A}$ - союзная матрица, она получена из исходной матрицы $A$ заменой ее элементов их алгебраическими дополнениями. Найдем $\tilde{A}$ , для этого вычислим алгебраические дополнения к элементам матрицы $A$ :

$A_{11}=(-1)^{1+1}\left|\begin{array}{rr}-1 & 0 \\ -1 & 2\end{array}\right|=-2$   $A_{12}=(-1)^{1+2}\left|\begin{array}{cc} 1 & 0 \\ 3 & 2 \end{array}\right|=-2$

$A_{13}=(-1)^{1+3}\left|\begin{array}{cc} 1 & -1 \\ 3 & -1 \end{array}\right|=2$    $A_{21}=(-1)^{2+1}\left|\begin{array}{rr} 1 & 1 \\ -1 & 2 \end{array}\right|=-3$

$A_{22}=(-1)^{2+2}\left|\begin{array}{cc} 2 & 1 \\ 3 & 2 \end{array}\right|=1$    $A_{23}=(-1)^{2+3}\left|\begin{array}{rr} 2 & 1 \\ 3 & -1 \end{array}\right|=5$

$A_{31}=(-1)^{3+1}\left|\begin{array}{rr} 1 & 1 \\ -1 & 0 \end{array}\right|=1$    $A_{32}=(-1)^{3+2}\left|\begin{array}{cc} 2 & 1 \\ 1 & 0 \end{array}\right|=1$

$A_{33}=(-1)^{3+3}\left|\begin{array}{rr} 2 & 1 \\ 1 & -1 \end{array}\right|=-3$

Таким образом,

$\tilde{A}=\left(\begin{array}{rrr} -2 & -2 & 2 \\ -3 & 1 & 5 \\ 1 & 1 & -3 \end{array}\right)$

Определитель матрицы $A$

$$\Delta=\left|\begin{array}{rrr} 2 & 1 & 1 \\ 1 & -1 & 0 \\ 3 & -1 & 2 \end{array}\right|=2 \cdot(-1) \cdot 2+1 \cdot(-1) \cdot 1+1 \cdot 0 \cdot 3-$$ $$-3 \cdot(-1) \cdot 1-(-1) \cdot 0 \cdot 2-1 \cdot 1 \cdot 2=-4 \neq 0$$

А тогда

$$\tilde{A}=-\frac{1}{4}\left(\begin{array}{rrr} -2 & -3 & 1 \\ -2 & 1 & 1 \\ 2 & 5 & -3 \end{array}\right)$$

Отсюда искомая матрица

$$X=\left(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}\right)=-\frac{1}{4}\left(\begin{array}{rrr} -2 & -3 & 1 \\ -2 & 1 & 1 \\ 2 & 5 & -3 \end{array}\right)\left(\begin{array}{r} 2 \\ -2 \\ 2 \end{array}\right)=$$ $$=\left(\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\right) \Rightarrow\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$$ $$\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$$

Задание. Найти решение СЛАУ $\left\{\begin{array}{l} 5 x_{1}+2 x_{2}=7 \\ 2 x_{1}+x_{2}=9 \end{array}\right.$ при помощи метода Крамера.

Решение. Вычисляем определитель матрицы системы:

$$\Delta=\left|\begin{array}{ll} 5 & 2 \\ 2 & 1 \end{array}\right|=5 \cdot 1-2 \cdot 2=1 \neq 0$$

Так как $\Delta \neq 0$ , то по теореме Крамера система совместна и имеет единственное решение. вычислим вспомогательные определители. Определитель $\Delta_{1}$ получим из определителя $\Delta$ заменой его первого столбца столбцом свободных коэффициентов. Будем иметь:

$$\Delta_{1}=\left|\begin{array}{ll} 7 & 2 \\ 9 & 1 \end{array}\right|=7-18=-11$$

Аналогично, определитель $\Delta_{2}$ получается из определителя матрицы системы $\Delta$ заменой второго столбца столбцом свободных коэффициентов:

$$\Delta_{2}=\left|\begin{array}{ll} 5 & 7 \\ 2 & 9 \end{array}\right|=45-14=31$$

Тогда получаем, что

$$x_{1}=\frac{\Delta_{1}}{\Delta}=\frac{-11}{1}=-11, x_{2}=\frac{\Delta_{2}}{\Delta}=\frac{31}{1}=31$$

Ответ. $x_{-1}=-11$, $x_{2} = 31$

Задание. При помощи формул Крамера найти решение системы $\left\{\begin{array}{l} 2 x_{1}+x_{2}+x_{3}=2 \\ x_{1}-x_{2}=-2 \\ 3 x_{1}-x_{2}+2 x_{3}=2 \end{array}\right.$

Решение. Вычисляем определитель матрицы системы:

$$\Delta=\left|\begin{array}{rrr} 2 & 1 & 1 \\ 1 & -1 & 0 \\ 3 & -1 & 2 \end{array}\right|=2 \cdot(-1) \cdot 2+1 \cdot(-1) \cdot 1+1 \cdot 0 \cdot 3-$$ $$-3 \cdot(-1) \cdot 1-(-1) \cdot 0 \cdot 2-1 \cdot 1 \cdot 2=-4 \neq 0$$

Так как определитель матрицы системы неравен нулю, то по теореме Крамера система совместна и имеет единственное решение. Для его нахождения вычислим следующие определители:

$$\Delta_{1}=\left|\begin{array}{rrr} 2 & 1 & 1 \\ -2 & -1 & 0 \\ 2 & -1 & 2 \end{array}\right|=2 \cdot(-1) \cdot 2+(-2) \cdot(-1) \cdot 1+$$ $$+1 \cdot 0 \cdot 2-2 \cdot(-1) \cdot 1-(-1) \cdot 0 \cdot 2-(-2) \cdot 1 \cdot 2=4$$ $$\Delta_{2}=\left|\begin{array}{rrr} 2 & 2 & 1 \\ 1 & -2 & 0 \\ 3 & 2 & 2 \end{array}\right|=2 \cdot(-2) \cdot 2+1 \cdot 2 \cdot 1+2 \cdot 0 \cdot 3-$$ $$-3 \cdot(-2) \cdot 1-2 \cdot 0 \cdot 2-1 \cdot 2 \cdot 2=-4$$ $$\Delta_{3}=\left|\begin{array}{rrr} 2 & 1 & 2 \\ 1 & -1 & -2 \\ 3 & -1 & 2 \end{array}\right|=2 \cdot(-1) \cdot 2+1 \cdot(-1) \cdot 2+$$ $$+1 \cdot(-2) \cdot 3-3 \cdot(-1) \cdot 2-(-1) \cdot(-2) \cdot 2-1 \cdot 1 \cdot 2=-12$$

Таким образом,

$x_{1}=\frac{\Delta_{1}}{\Delta}=\frac{4}{-4}=-1$    $x_{2}=\frac{\Delta_{2}}{\Delta}=\frac{-4}{-4}=1$    $x_{3}=\frac{\Delta_{3}}{\Delta}=\frac{-12}{-4}=3$

Ответ. $\left\{\begin{array}{l}x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3\end{array}\right.$

Задание. Решить СЛАУ $\left\{\begin{array}{l} 2 x_{1}+x_{2}+x_{3}=2 \\ x_{1}-x_{2}=-2 \\ 3 x_{1}-x_{2}+2 x_{3}=2 \end{array}\right.$ методом Гаусса.

Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент $a_{1}$ равнялся 1 (это мы делаем для упрощения вычислений):

$$\tilde{A}=A \mid B=\left(\begin{array}{rrr|r} 2 & 1 & 1 & 2 \\ 1 & -1 & 0 & -2 \\ 3 & -1 & 2 & 2 \end{array}\right) \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 2 & 1 & 1 & 2 \\ 3 & -1 & 2 & 2 \end{array}\right)$$

Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей - три первых:

$$\tilde{A} \sim\left(\begin{array}{ccc|c} 1 & -1 & 0 & -2 \\ 0 & 3 & 1 & 6 \\ 0 & 2 & 2 & 8 \end{array}\right)$$

Все элементы третьей строки делим на два (или, что тоже самое, умножаем на $\frac{1}{2}$:

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 3 & 1 & 6 \\ 0 & 1 & 1 & 4 \end{array}\right)$$

Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 3 & 1 & 6 \end{array}\right)$$

От третьей строки отнимаем вторую, умноженную на 3:

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & -2 & -6 \end{array}\right)$$

Умножив третью строку на $\left(-\frac{1}{2}\right)$ , получаем:

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & 1 & 3 \end{array}\right)$$

Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент $$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 3 \end{array}\right)$$

Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:

$$\tilde{A} \sim\left(\begin{array}{ccc|c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 3 \end{array}\right)$$

Полученной матрице соответствует система

$\left\{\begin{array}{l} x_{1}+0 \cdot x_{2}+0 \cdot x_{3}=-1 \\ 0 \cdot x_{1}+x_{2}+0 \cdot x_{3}=1 \\ 0 \cdot x_{1}+0 \cdot x_{2}+x_{3}=3 \end{array}\right.$    или    $\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$

Ответ. $\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$

Задание. Выяснить, имеет ли однородная СЛАУ $\left\{\begin{array}{l} 3 x-2 y=-1 \\ x+3 y=7 \end{array}\right.$ ненулевые решения.

Решение. Вычислим определитель матрицы системы:

$$\Delta=\left|\begin{array}{rr} 3 & -2 \\ 1 & 3 \end{array}\right|=9-(-2)=9+2=11 \neq 0$$

Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$

Ответ. Система имеет только нулевое решение.

Задание. Найти общее решение и ФСР однородной системы $\Delta=\left|\begin{array}{rr} 3 & -2 \\ 1 & 3 \end{array}\right|=9-(-2)=9+2=11 \neq 0$

Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

$$A=\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 1 & -2 & 2 & -1 & 0 \\ 4 & -2 & 6 & 3 & -4 \\ 2 & 4 & -2 & 4 & -7 \end{array}\right)$$

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей - четыре первых, от четвертой - две первых:

$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & -6 & 6 & 15 & 0 \\ 0 & 2 & -2 & 10 & -5 \end{array}\right)$$

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:

$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 9 & -3 \\ 0 & 0 & 0 & 12 & -4 \end{array}\right)$$

От четвертой строки отнимем $$\frac{4}{3}$$ третьей и третью строку умножим на $$\frac{1}{3}$$ :

$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right)$$

Нулевые строки можно далее не рассматривать, тогда получаем, что

$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \end{array}\right)$$

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:

$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -6 & 0 \\ 0 & -2 & 2 & 5 & 0 \\ 0 & 0 & 0 & 3 & -1 \end{array}\right)$$

то есть получаем систему, соответствующую данной матрице:

$$\left\{\begin{array}{l} x_{1}+x_{2}-6 x_{4}=0 \\ -2 x_{2}+2 x_{3}+5 x_{4}=0 \\ 3 x_{4}-x_{5}=0 \end{array}\right.$$

Или, выразив одни переменные через другие, будем иметь:

$$\left\{\begin{array}{l} x_{1}=-x_{2}+6 x_{4} \\ x_{2}=x_{2} \\ x_{3}=x_{2}-\frac{5}{2} x_{4} \\ x_{4}=x_{4} \\ x_{5}=3 x_{4} \end{array}\right.$$

Здесь $x_{2}, x_{4}$ - независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_{1},x_{3},x_{5}$ - зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ - количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$

Так как ранг матрицы $r=3$ , а количество неизвестных системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3-2$ (для проверки, это число должно равняться количеству свободных переменных).

Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

$$\left\{\begin{array}{l} x_{1}=-x_{2}+6 x_{4} \\ x_{3}=x_{2}-\frac{5}{2} x_{4} \\ x_{5}=3 x_{4} \end{array}\right.$$

Тогда придавая в первом случае, например, независимым переменным значения $x_{2}=1$ , $x_{4}=0$ получаем, что $\left\{\begin{array}{l} x_{1}=-1+6 \cdot 0=-1 \\ x_{3}=1-\frac{5}{2} \cdot 0=1 \\ x_{5}=3 \cdot 0=0 \end{array}\right.$ . Полученные значения записываем в первую строку таблицы. Аналогично, беря $x_{2}=0$ , $x_{4}=2$, будем иметь, что $x_{1}=12,x_{3}=-5,x_{5}=6$ , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:

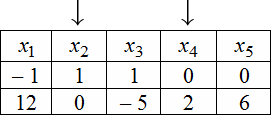
Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

$$\left\{\begin{array}{l} x_{1}=-1+6 \cdot 0=-1 \\ x_{3}=1-\frac{5}{2} \cdot 0=1 \\ x_{5}=3 \cdot 0=0 \end{array}\right.$$

Общее решение является линейной комбинацией частных решений:

$$X=C_{1} X_{1}+C_{2} X_{2}=C_{1}\left(\begin{array}{r} -1 \\ 1 \\ 1 \\ 0 \\ 0 \end{array}\right)+C_{2}\left(\begin{array}{r} 12 \\ 0 \\ -5 \\ 2 \\ 6 \end{array}\right)$$

где коэффициенты $C_{1}, C_{2}$ не равны нулю одновременно. Или запишем общее решение в таком виде:

$\left\{\begin{array}{l} x_{1}=-C_{1}+12 C_{2} \\ x_{2}=C_{1} \\ x_{3}=C_{1}-5 C_{2} \\ x_{4}=2 C_{2} \\ x_{5}=6 C_{2} \end{array}\right.$    $C_{1}, C_{2} \neq 0$

Придавая константам $C_{1}, C_{2}$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.