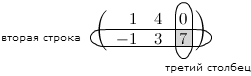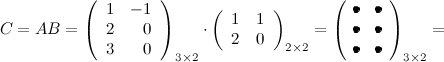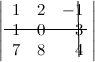Примеры решения задач с матрицами

Задание. Чему равен элемент $ a_{23} $ матрицы $ A=\left( \begin{array}{rrr}{1} & {4} & {0} \\ {-1} & {3} & {7}\end{array}\right) $ ?

Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:

Таким образом, $a_{23}=7$.

Ответ. $a_{23}=7$

Задание. Пусть $A=\left( \begin{array}{r}{3} \\ {-1}\end{array}\right)$ . Найти матрицу 2$A$.

Решение. $2 A=2 \cdot \left( \begin{array}{r}{3} \\ {-1}\end{array}\right)=\left( \begin{array}{c}{2 \cdot 3} \\ {2 \cdot(-1)}\end{array}\right)=\left( \begin{array}{r}{6} \\ {-2}\end{array}\right)$

Ответ. $2 A=\left( \begin{array}{r}{6} \\ {-2}\end{array}\right)$

Задание. Найти $A+B$, если $A=\left( \begin{array}{rrr}{1} & {-2} & {4} \\ {2} & {0} & {-1}\end{array}\right)$, $B=\left( \begin{array}{lll}{5} & {2} & {3} \\ {4} & {6} & {2}\end{array}\right)$

Решение. $C=A+B=\left( \begin{array}{rrr}{1} & {-2} & {4} \\ {2} & {0} & {-1}\end{array}\right)+\left( \begin{array}{lll}{5} & {2} & {3} \\ {4} & {6} & {2}\end{array}\right)=$

$=\left( \begin{array}{rrr}{1+5} & {-2+2} & {4+3} \\ {2+4} & {0+6} & {-1+2}\end{array}\right)=\left( \begin{array}{lll}{6} & {0} & {7} \\ {6} & {6} & {1}\end{array}\right)$

Ответ. $C=\left( \begin{array}{lll}{6} & {0} & {7} \\ {6} & {6} & {1}\end{array}\right)$

Задание. Найти матрицу $C=A-3 B$, если $A=\left( \begin{array}{rr}{1} & {2} \\ {2} & {-1} \\ {3} & {0}\end{array}\right), B=\left( \begin{array}{rr}{-1} & {1} \\ {1} & {2} \\ {0} & {0}\end{array}\right)$

Решение. $C=A-3 B=\left( \begin{array}{rr}{1} & {2} \\ {2} & {-1} \\ {3} & {0}\end{array}\right)-3 \cdot \left( \begin{array}{rr}{-1} & {1} \\ {1} & {2} \\ {0} & {0}\end{array}\right)=$

$\left( \begin{array}{rr}{1} & {2} \\ {2} & {-1} \\ {3} & {0}\end{array}\right)-\left( \begin{array}{rr}{-3} & {3} \\ {3} & {6} \\ {0} & {0}\end{array}\right)=\left( \begin{array}{cc}{1-(-3)} & {2-3} \\ {2-3} & {-1-6} \\ {3-0} & {0-0}\end{array}\right)=\left( \begin{array}{rr}{4} & {-1} \\ {-1} & {-7} \\ {3} & {0}\end{array}\right)$

Ответ. $C=\left( \begin{array}{rr}{4} & {-1} \\ {-1} & {-7} \\ {3} & {0}\end{array}\right)$

Задание. Вычислить $A B$ и $B A$, если $A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right), B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)$

Решение. Так как $A=A_{3 \times 2}$ , а $B=B_{2 \times 2}$ , то произведение возможно и результатом операции умножения будет матрица $C=C_{3 \times 2}$ , а это матрица вида $C=\left( \begin{array}{cc}{c_{11}} & {c_{12}} \\ {c_{21}} & {c_{22}} \\ {c_{31}} & {c_{32}}\end{array}\right)$ .

Вычисли элементы матрицы $C$ :

$ c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}=1 \cdot 1+(-1) \cdot 2=-1 $

$ c_{12}=a_{11} \cdot b_{12}+a_{12} \cdot b_{22}=1 \cdot 1+(-1) \cdot 0=1 $

$ c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}=2 \cdot 1+0 \cdot 2=2 $

$ c_{22}=a_{21} \cdot b_{12}+a_{22} \cdot b_{22}=2 \cdot 1+0 \cdot 0=2 $

$ c_{31}=a_{31} \cdot b_{11}+a_{32} \cdot b_{21}=3 \cdot 1+0 \cdot 2=3 $

$ c_{31}=a_{31} \cdot b_{12}+a_{32} \cdot b_{22}=3 \cdot 1+0 \cdot 0=3 $

Итак, $C=A B=\left( \begin{array}{rl}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ .

Выполним произведения в более компактном виде:

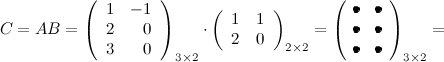
$=\left( \begin{array}{rrr}{1 \cdot 1+(-1) \cdot 2} & {1 \cdot 1+(-1) \cdot 0} \\ {2 \cdot 1+0 \cdot 2} & {2 \cdot 1+0 \cdot 0} \\ {3 \cdot 1+0 \cdot 2} & {3 \cdot 1+0 \cdot 0}\end{array}\right)=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$

Найдем теперь произведение $D=B A=B_{2 \times 2} \cdot A_{3 \times 2}$. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.

Ответ. $A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы $B$ не совпадает с количеством строк матрицы $A$ .

Задание. Найти матрицу $A^{T}$, если $A=\left( \begin{array}{rl}{1} & {0} \\ {-2} & {3}\end{array}\right)$

Решение. $A^{T}=\left( \begin{array}{rr}{1} & {0} \\ {-2} & {3}\end{array}\right)^{T}=\left( \begin{array}{rr}{1} & {-2} \\ {0} & {3}\end{array}\right)$

Ответ. $A^{T}=\left( \begin{array}{rr}{1} & {-2} \\ {0} & {3}\end{array}\right)$

Задание. Найти минор $M_{23}$ к элементу $a_{23}$ определителя $\left| \begin{array}{rrr}{1} & {2} & {-1} \\ {1} & {0} & {3} \\ {7} & {8} & {4}\end{array}\right|$ .

Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:

тогда $M_{23}=\left| \begin{array}{ll}{1} & {2} \\ {7} & {8}\end{array}\right|$

Ответ. $M_{23}=\left| \begin{array}{ll}{1} & {2} \\ {7} & {8}\end{array}\right|$

Задание. Найти алгебраическое дополнение $A_{23}$ к элементу $a_{23}$ определителя $\left| \begin{array}{rrr}{1} & {2} & {-1} \\ {1} & {0} & {3} \\ {7} & {8} & {4}\end{array}\right|$ .

Решение. $A_{23}=(-1)^{2+3} \cdot M_{23}=(-1)^{5} \cdot \left| \begin{array}{ll}{1} & {2} \\ {7} & {8}\end{array}\right|=-\left| \begin{array}{ll}{1} & {2} \\ {7} & {8}\end{array}\right|$

Ответ. $A_{23}=-\left| \begin{array}{ll}{1} & {2} \\ {7} & {8}\end{array}\right|$

Задание. Вычислить определитель второго порядка $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|$

Решение. $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|=11 \cdot 5-(-2) \cdot 7=55+14=69$

Ответ. $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|=69$

Задание. Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ методом треугольников.

Решение. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=3 \cdot 1 \cdot(-2)+4 \cdot(-2) \cdot(-1)+$

Ответ. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=54$

Задание. Вычислить определитель $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|$

Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.

Определитель равен нулю, так как вторая и третья строки являются пропорциональными.

Ответ. $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=0$

Задание. Вычислить определитель $\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|$ приведением его к треугольному виду.

Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_{11}$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:

Далее получим нули в первом столбце, кроме элемента $a_{11}$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:

Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен $\pm 1$ , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):

Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой - две вторых строки, получаем:

Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:

Ответ. $\Delta=-80$

Задание. Для матрицы $A=\left( \begin{array}{ll}{7} & {4} \\ {5} & {3}\end{array}\right)$ найти обратную методом присоединенной матрицы.

Решение. Приписываем к заданной матрице $A$ справа единичную матрицу второго порядка:

От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):

От второй строки отнимаем две первых:

Первую и вторую строки меняем местами:

От второй строки отнимаем две первых:

Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:

Итак, слева получили единичную матрицу, а значит матрица, стоящая в правой части (справа от вертикальной черты), является обратной к исходной.

Таким образом, получаем, что $A^{-1}=\left( \begin{array}{rr}{3} & {-4} \\ {-5} & {7}\end{array}\right)$

Ответ. $A^{-1}=\left( \begin{array}{rr}{3} & {-4} \\ {-5} & {7}\end{array}\right)$

Задание. Найти обратную матрицу для $A=\left( \begin{array}{ll}{1} & {1} \\ {1} & {2}\end{array}\right)$

Решение. Шаг 1. Находим определитель: $\Delta=\left| \begin{array}{ll}{1} & {1} \\ {1} & {2}\end{array}\right|=2-1=1 \neq 0$

Шаг 2. $A^{\prime}=\left( \begin{array}{rr}{2} & {-1} \\ {-1} & {1}\end{array}\right)$

Шаг 3. $A^{-1}=\frac{1}{\Delta} \cdot A^{\prime}=\left( \begin{array}{rr}{2} & {-1} \\ {-1} & {1}\end{array}\right)$

Ответ. $A^{-1}=\left( \begin{array}{rr}{2} & {-1} \\ {-1} & {1}\end{array}\right)$

Задание. Найти обратную матрицу к матрице $A=\left( \begin{array}{rrr}{1} & {0} & {2} \\ {2} & {-1} & {1} \\ {1} & {3} & {-1}\end{array}\right)$

Решение. Вычисляем определитель матрицы:

Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица $A^{-1}$ к матрице $A$ находится по формуле:

Найдем союзную матрицу $\check{A}$ , для этого вычислим алгебраические дополнения к элементам матрицы $A$ :

Таким образом, $\tilde{A}=\left( \begin{array}{rrr}{-2} & {3} & {7} \\ {6} & {-3} & {-3} \\ {2} & {3} & {-1}\end{array}\right)$

Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):

Итак, $A^{-1}=\frac{1}{12} \left( \begin{array}{rrr}{-2} & {6} & {2} \\ {3} & {-3} & {3} \\ {7} & {-3} & {-1}\end{array}\right)$

Ответ. $A^{-1}=\frac{1}{12} \left( \begin{array}{rrr}{-2} & {6} & {2} \\ {3} & {-3} & {3} \\ {7} & {-3} & {-1}\end{array}\right)$

Задание. Найти ранг матрицы $A=\left( \begin{array}{cccc}{0} & {4} & {10} & {1} \\ {4} & {8} & {18} & {7} \\ {10} & {18} & {40} & {17} \\ {1} & {7} & {17} & {3}\end{array}\right)$

Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:

От второй строки отнимаем четвертую строку, умноженную на 4; от третьей - две четвертых:

Ко второй строке прибавим пять первых, к третьей - три третьих:

Меняем местами первую и вторую строчки:

Далее четвертую и первую строки:

Ответ. $\operatorname{rang} A=2$

Задание. Найти ранг матрицы $A=\left( \begin{array}{rrrr}{1} & {2} & {-1} & {-2} \\ {2} & {4} & {3} & {0} \\ {-1} & {-2} & {6} & {6}\end{array}\right)$ , используя метод окаймления миноров.

Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам матрицы $A$ . Рассмотрим, например, минор $M_{1}=1 \neq 0$ . расположенный в первой строке и первом столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор $M_{2}^{1}=\left| \begin{array}{ll}{1} & {2} \\ {2} & {4}\end{array}\right|=0$ ; рассмотрим еще один минор второго порядка, для этого минор $M_{1}$ окаймляем при помощи второй строки и третьего столбца, тогда имеем минор $M_{2}^{2}=\left| \begin{array}{rr}{1} & {-1} \\ {2} & {3}\end{array}\right|=5 \neq 0$ , то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор $M_{2}^{2}$ . Таких миноров два: комбинация третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:

так как содержит два пропорциональных столбца (первый и второй); второй минор

преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:

И так как первая и вторая строки пропорциональны, то минор равен нулю.

Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы $A$ равен двум: $\operatorname{rang} A=2$

Ответ. $\operatorname{rang} A=2$