Минором $M_{i j}$ к элементу $a_{i j}$ определителя $n$-го порядка называется определитель $(n-1)$-го порядка, полученный из исходного вычеркиванием $i$-той строки и $j$-того столбца.
Содержание:
Минор
Определение
Пример
Задание. Найти минор $ M_{23} $ к элементу $ a_{23} $ определителя $ \left| \begin{array}{rrr}{1} & {2} & {-1} \\ {1} & {0} & {3} \\ {7} & {8} & {4}\end{array}\right| $ .
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
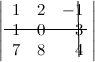
тогда $ M_{23}=\left| \begin{array}{ll}{1} & {2} \\ {7} & {8}\end{array}\right| $
Ответ. $ M_{23}=\left| \begin{array}{ll}{1} & {2} \\ {7} & {8}\end{array}\right| $
Алгебраическое дополнение
Определение
Алгебраическим дополнением $ A_{i j} $ к элементу $ a_{i j} $ определителя $n$-го порядка называется число $ A_{i j}=(-1)^{i+j} \cdot M_{i j} $
Пример
Задание. Найти алгебраическое дополнение $ A_{23} $ к элементу $ a_{23} $ определителя $ \left| \begin{array}{rrr}{1} & {2} & {-1} \\ {1} & {0} & {3} \\ {7} & {8} & {4}\end{array}\right| $ .
Решение. $ A_{23}=(-1)^{2+3} \cdot M_{23}=(-1)^{5} \cdot \left| \begin{array}{ll}{1} & {2} \\ {7} & {8}\end{array}\right|=-\left| \begin{array}{ll}{1} & {2} \\ {7} & {8}\end{array}\right| $
Ответ. $ A_{23}=-\left| \begin{array}{ll}{1} & {2} \\ {7} & {8}\end{array}\right| $
Сумма произведений элементов "произвольной" строки на алгебраические дополнения к элементам $i$-ой строки определителя равна определителю, в котором вместо $i$-ой строки записана "произвольная" строка.
$$ b_{1} \cdot A_{11}+b_{2} \cdot A_{12}+b_{3} \cdot A_{13}=\left| \begin{array}{ccc}{b_{1}} & {b_{2}} & {b_{3}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right| $$
Сумма произведений элементов строки определителя на алгебраические дополнения к элементам другой строки равна нулю.
$$ a_{31} \cdot A_{11}+a_{32} \cdot A_{12}+a_{33} \cdot A_{13}=\left| \begin{array}{ccc}{a_{31}} & {a_{32}} & {a_{33}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|=0 $$
Читать дальше: методы вычисления определителей.










