Если десятичных знаков дроби меньше, чем количество нулей у единицы, то на пустые места записывают нули.
Содержание:
- Умножение и деление десятичной дроби на 10, 100, 1000 и т.д.
- Сложение и вычитание десятичных дробей
- Умножение десятичных дробей
- Деление десятичных дробей
Умножение и деление десятичной дроби на 10, 100, 1000 и т.д.
Чтобы умножить десятичную дробь на 10, 10, 1000 и т.д. надо перенести десятичную запятую на столько знаков вправо, сколько нулей содержит число 10, 100, 1000 и т.д.
Замечание
Пример
Задание. Выполнить умножение: 1) $2,34 \cdot 10$ ; 2) $2,34 \cdot 100$ ; 3) $2,34 \cdot 1000$
Решение. 1) Так заданная дробь умножается на 10 (один нуль), то десятичную запятую переносим на один знак вправо:
$$2,34 \cdot 10=23,4$$2) Число умножается на 100, поэтому десятичную запятую переносим на два знака вправо:
$$2,34 \cdot 100=234$$3) В данном случае запятую у десятичной дроби надо перенести на три знака вправо, и так как дробь содержит только два десятичных знака, то справа дописываем один нуль:
$$2,34 \cdot 1000=2340$$Чтобы поделить десятичную дробь на 10, 100, 1000 и т.д., надо перенести десятичную запятую на один, два, три и т.д. знака влево соответственно.
Замечание
Если для перенесения запятой в дроби не хватает знаков, их число дополняют соответствующим количеством нулей слева.
Пример
Задание. Выполнить действия: 1) $23,4 : 10$ ; 2) $23,4 : 100$ ; 3) $23,4 : 1000$
Решение. 1) Переносим запятую на один знак влево, так как делим на 10 и это число содержит один нуль. Будем иметь:
$$23,4 : 10=2,34$$2) В этом случае при делении на 100 переносим запятую на два знака влево:
$$23,4 : 100=0,234$$3) Запятая переносится на три знака влево, недостающий один знаки дополняем одним нулем. Получаем:
$$23,4 : 1000=0,0234$$Сложение и вычитание десятичных дробей
При сложении (вычитании) десятичных дробей поступают следующим образом:
-
При необходимости уравнивают количество знаков после запятой, добавляя справа нули к соответствующей дроби, что, согласно основному свойству десятичных дробей, не влияет на величину дроби.
Например. Если надо, например, сложить дроби $0,123$ и $4,56$ , то справа ко второй дроби надо дописать один нуль, чтобы десятичных знаков стало три: $4,560$
-
Записывают дроби так, чтобы их запятые находились друг под другом (или, что то же самое, разряд под разрядом).
Например. Правильная запись:
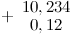
Неправильная запись:
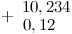 или
или
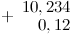
- Сложить/вычесть, не обращая внимания на запятую, как целые числа. Складываем по одной цифре, начиная с самого крайнего правого разряда и двигаясь влево к следующему
- Поставить запятую в сумме/разности под запятыми, складываемых/вычитаемых дробей.
Пример
Задание. Найти сумму дробей $32,45$ и $4,274$
Решение. Распишем решение пошагово. Итак, нам надо найти сумму
$$32,45+4,274$$Действия будем производить в столбик, то есть запишем сумму следующим образом (помним, что для десятичных дробей при выполнении сложения/вычитания десятичные запятые дробей должны находиться на одной вертикальной линии):
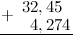
Вначале к первой дроби справа дописываем нуль, чтобы уравнять количество десятичных знаков:
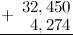
Складываем по одной цифре (знаку, разряду) справа налево. Результат сложения записываем под соответствующими
слагаемыми под чертой. На первом этапе складываем 0 и 4: 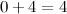 :
:
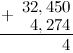
Теперь складываем 5 и 7: 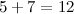 , в результате получилось
число большее 10, а поэтому под чертой записываем только последнюю цифру полученного числа, то есть 2, а над соседним левым
разрядом - 4 - ставим оставшиеся цифры, то есть 1. (Обычно при решении говорят так: "два пишем, один в уме"):
, в результате получилось
число большее 10, а поэтому под чертой записываем только последнюю цифру полученного числа, то есть 2, а над соседним левым
разрядом - 4 - ставим оставшиеся цифры, то есть 1. (Обычно при решении говорят так: "два пишем, один в уме"):
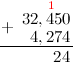
Единица над 4 означает, что после того как будет выполнено сложение следующего разряда:
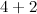 , к полученной сумме надо будет прибавить 1,
которую мы "держим в уме".
, к полученной сумме надо будет прибавить 1,
которую мы "держим в уме".
Итак, складываем далее, к 4 прибавляем 2: 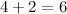 и
прибавляем "красную" единицу:
и
прибавляем "красную" единицу: 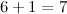 . То есть под чертой под десятыми пишем 7:
. То есть под чертой под десятыми пишем 7:
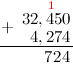
Под десятичными запятыми слагаемых, ставим запятую суммы:
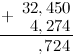
И продолжаем сложение далее по выше описанному алгоритму: 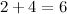 :
:
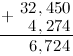
И, снеся 3 (под ней во втором слагаемом нет соответствующей цифры), окончательно будем иметь:
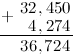
Таким образом, $32,45+4,274=36,724$
Ответ. $32,45+4,274=36,724$
Пример
Задание. Вычислить $4,312-0,91$
Решение. Выполним вычитание в столбик, для этого запишем заданные десятичные дроби одна под другой так, чтобы их десятичные запятые находились на одной вертикали:
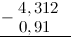
Для того, чтобы десятичных знаков было равное число, допишем ко второй дроби справа нуль:
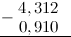
Вычитание столбиком начинаем с самой правой цифры: 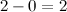 . результат записываем под чертой:
. результат записываем под чертой:
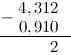
Далее от 1 отнимаем 1:
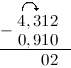
Теперь нам нужно вычесть из тройки девять. Это сделать нельзя, так как #3 < 9# . Поэтому "займем десяток" в соседнем слева от 3 разряде - у 4. Это действие отметим стрелкой сверху. Занятый десяток прибавим к 3: $3+10=13$ . Соответственно 4 уменьшилась на 1: $4-1=3$ . Итак, далее из 13 вычтем 9: $3-9=4$ :
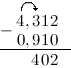
Далее ставим запятую:
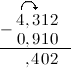
Далее от 3 (то, что осталось от 4, после того, как мы забрали нее одну единицу) отнимем 0:
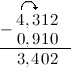
Итак, в итоге получаем, что $4,312-0,91=3,402$
Ответ. $4,312-0,91=3,402$
Умножение десятичных дробей
Чтобы умножить одно десятичное число на другое, необходимо перемножить их как целые числа, не обращая внимания на запятые, а затем в полученном произведении отделить справа столько десятичных знаков, сколько их было вместе в обоих сомножителях.
Пример
Задание. Вычислить $2,34 \cdot 4,12$
Решение. Умножаем заданные числа, не обращая внимания на запятые:
$234 \cdot 412 = 96408$Так как первый множитель содержит два десятичных знака и второй также, то у результата отделяем $2+2=4$ знака справа:
$2,34 \cdot 4,12 = 9,6408$Ответ. $2,34 \cdot 4,12 = 9,6408$
Деление десятичных дробей
Для деления десятичной дроби на натуральное число придерживаются следующего алгоритма:
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимание на запятую.
- Ставим в полученном частном запятую, когда заканчивается деление целой части делимого. Если целая часть делимого меньше делителя, то в частном ставим 0 целых.
Пример
Задание. Выполнить деление $1,176:21$
Решение. Так как целая часть десятичной дроби, которая равна 1, меньше, чем делитель, который равен 21, то в частном в целой части ставим 0. Далее делим как целые числа:

Таким образом, $1,176:21 = 0,056$
Ответ. $1,176:21 = 0,056$
Для того, чтобы поделить число на десятичную дробь, необходимо делитель превратить в целое число, умножив его на 10, 100, 1000 и т.д. раз соответственно. Чтобы величина дроби не изменилась, на это же число (10, 100, 1000 и т.д.) надо умножить и делимое, после чего деление сведется к делению на целое число, алгоритм которого описан выше.
Пример
Задание. Поделить дробь $1,23$ на дробь $0,3$
Решение. Так как делитель $0,3$ не является целым числом, то его надо таковым сделать. Так как у данного числа один знак после запятой, тогда для перемещения десятичной запятой вправо на один знак его (число) надо умножить на 10: $0,3 \cdot 10=3$ . Чтобы результат не изменился, надо и делимое $0,3$ умножить на 10: $1,23 \cdot 10=12,3$
Таким образом, пришли к равносильному делению $12,3:3$ . Деление произведем в столбик:
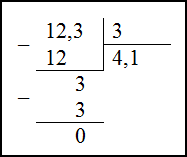
Ответ. $1,23:0,3 = 4,1$
Читать следующую тему: периодические десятичные дроби.










