Содержание:

Определение

Десятичной дробью называют обыкновенную дробь, знаменателем которой является единица с последующими нулями.

Например.  $\frac{3}{10}, 4 \frac{7}{100}, \frac{11}{10000}$

Такие дроби обычно записывают без знаменателя, а значение каждой цифры зависит от места, на котором она стоит. Для таких дробей целая часть отделяется запятой, а после запятой должно быть столько цифр, сколько нулей имеет единица в знаменателе обыкновенной дроби. Цифры дробной части называются десятичными знаками.

Например.  $\frac{21}{100}=0,21 ; 3 \frac{21}{100}=3,21$

Первый десятичный знак после запятой соответствует десятым, второй - сотым, третий - тысячным и т.д.

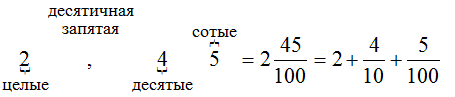
Если количество нулей в знаменателе десятичной дроби больше, чем количество цифр в числителе этой же дроби, то после десятичной запятой перед цифрами числителя дописывается нужное количество нулей.

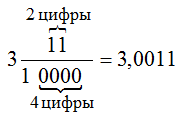
Так как нулей в знаменателе четыре штуки, а цифр в числителе две, то в десятичной записи дроби перед числителем дописываем $4-2=2$ нуля.

Основное свойство десятичной дроби

Свойство

Если к десятичной дроби справа дописать несколько нулей, то величина десятичной дроби не изменится.

Например.  $12,034=12,0340=12,03400=12,034000=\ldots$

Замечание

Таким образом, нули в конце десятичной дроби не учитываются, поэтому при выполнении различных действий эти нули можно зачеркнуть/отбросить.

Сравнение десятичных дробей

Чтобы сравнить две десятичные дроби (выяснить, какая из двух десятичных дробей больше), надо сравнить их целые части, затем десятые, сотые и т.д. Если целая часть одной из дробей больше целой части другой дроби, то первая дробь считается большей. В случае равенства целых частей больше та дробь, у которой десятых больше и т.д.

Пример

Задание. Сравнить дроби $2,432$ ; $2,41$ и $1,234$

Решение. Дробь $1,234$ является самой меньшей, так как ее целая часть равна 1, а $1 \lt 2$ , где 2 - целая часть двух оставшихся дробей $2,432$ и $1,234$ .

Сравним теперь по величине дроби $2,432$ и $1,234$ . Их целые части равны между собой и равны 2. Сравниваем десятые: $4=4$ . Сравниваем сотые: $3>1$ . Таким образом, $2,432>2,41$ .

Итак, окончательно имеем: $1,234 \lt 2,41 \lt 2,432$

Ответ.   $1,234 \lt 2,41 \lt 2,432$

Читать следующую тему: превращение десятичной дроби в обыкновенную и наоборот.

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 451 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!