Задание. Найти произведение $\frac{1}{3} \cdot 4$
Решение. Выполним умножение по описанному выше правилу
$\frac{1}{3} \cdot 4=\frac{1 \cdot 4}{3}=\frac{4}{3}=1 \frac{1}{3}$
Ответ. $\frac{1}{3} \cdot 4=1 \frac{1}{3}$
Содержание:
Умножение дроби $\frac{a}{b}$ на число $n$ равносильно сложению одинаковых слагаемых:
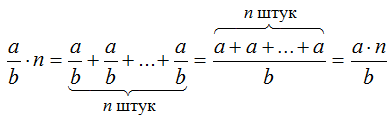
Итак, можно сделать вывод, что чтобы умножить дробь на число, надо числитель этой дроби умножить на это число, а знаменатель оставить без изменения.
Пример
Задание. Найти произведение $\frac{1}{3} \cdot 4$
Решение. Выполним умножение по описанному выше правилу
$\frac{1}{3} \cdot 4=\frac{1 \cdot 4}{3}=\frac{4}{3}=1 \frac{1}{3}$
Ответ. $\frac{1}{3} \cdot 4=1 \frac{1}{3}$
Аналогично выполняется умножения числа на дробь.
Пример
Задание. Найти произведение 3$\cdot \frac{1}{4}$
Решение. Выполним умножение по описанному выше правилу
$3 \cdot \frac{1}{4}=\frac{3 \cdot 1}{4}=\frac{3}{4}$
Ответ. $3 \cdot \frac{1}{4}=\frac{3}{4}$
Определение
Произведением дробей называется такая дробь, числитель которой равен произведению числителей исходных дробей, а знаменатель - произведению их знаменателей:
$\frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}$
Таким образом, чтобы умножить дробь на дробь, надо умножить числитель первой дроби на числитель второй и результат записать в числитель; а также перемножить знаменатели и результат записать в знаменатель.
Замечание. При выполнении умножения по возможности следует сокращать. Сокращать можно только числа стоящие в числителе с числами, стоящими в знаменателе. Числитель с числителем и знаменатель со знаменателем сокращать нельзя.
Пример
Задание. Найти произведение дробей $\frac{1}{3}$ и $\frac{4}{5}$
Решение. Выполним умножение дробей по описанному выше правилу
$\frac{1}{3} \cdot \frac{4}{5}=\frac{1 \cdot 4}{3 \cdot 5}=\frac{4}{15}$
Ответ. $\frac{1}{3} \cdot \frac{4}{5}=\frac{4}{15}$
Пример
Задание. Умножить $\frac{13}{14}$ на $\frac{14}{39}$
Решение. Необходимо найти произведение $\frac{13}{14} \cdot \frac{14}{39}$ . Как видим, числа 13 и 39 можно сократить на общее число 13. Для этого сами указанные величины зачеркиваем, а над ними пишем число, которое получается после деления. Аналогично поступает со знаменателем первой дроби и числителем второй:
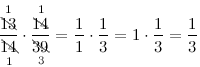
Ответ. $\frac{13}{14} \cdot \frac{14}{39}=\frac{1}{3}$
Чтобы перемножить смешанные дроби, нужно представить их в виде неправильных дробей, а затем уже выполнить умножение как обыкновенных дробей.
Пример
Задание. Найти произведение дробей 3$\frac{1}{3} \cdot 4 \frac{2}{5}$
Решение. Выполним умножение смешанных дробей по описанному выше правилу
$3 \frac{1}{3} \cdot 4 \frac{2}{5}=\frac{3 \cdot 3+1}{3} \cdot \frac{4 \cdot 5+2}{5}=\frac{10}{3} \cdot \frac{22}{5}=$
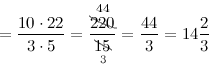
Ответ. $3 \frac{1}{3} \cdot 4 \frac{2}{5}=14 \frac{2}{3}$
Для умножения смешанной дроби на целое число поступают либо аналогично и далее умножают дробь на число, либо на целое число отдельно умножают целую часть, и отдельно дробную часть смешанного числа.
Пример
Задание. Умножить смешанную дробь 3$\frac{3}{4}$ на 2
Решение. Выполним умножение смешанной дроби на число по описанному выше правилу
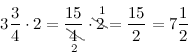
Либо
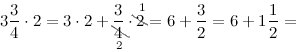
$=(6+1)+\frac{1}{2}=7+\frac{1}{2}=7 \frac{1}{2}$
Ответ. $3 \frac{3}{4} \cdot 2=7 \frac{1}{2}$
Читать следующую тему: деление дробей.