Бесконечная десятичная дробь, у которой одна или несколько цифр повторяются в одной и той же последовательности, называется периодической десятичной дробью.
Определение
Например. $0,1234444444 \ldots ; 12,453737373737 \ldots$
Повторяющиеся цифры - период - для сокращения записи пишут в круглых скобках.
Например. $0,12344444444 \ldots=0,123(4)$ ; $12,453737373737 \ldots=12,45(37)$
Определение
Чистой периодической дробью называется периодическая дробь, у которой период начинается сразу после запятой.
Например. $2,4949 \ldots=2,(49)$
Определение
Смешанной периодической дробью называется такая десятичная дробь, у которой между запятой и периодом есть не менее одной неповторяющейся бесконечное число раз цифры.
Например. $0,11232323 \ldots=0,11(23)$ ; $1,54444 . .=1,5(4)$
Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период, а в знаменателе записать столько девяток, сколько цифр в периоде.
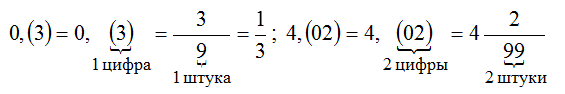
Чтобы записать смешанную периодическую дробь в виде обыкновенной, надо из числа, стоящего до второго периода вычесть число, стоящее до первого периода, результат записать в числителе; в знаменатель записать число, содержащее столько девяток, сколько цифр в периоде, и столько нулей в конце, сколько цифр между запятой и периодом.
Например. Запишем дробь $2,34(2)$ в виде обыкновенной
Читать первую тему - понятие дроби и виды дробей, раздела дроби.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
Статьи по теме
Поможем выполнить
любую работу
