Содержание:

Определение

Множество целых чисел - это множество, которое образовано добавлением к множеству натуральных чисел новых объектов-чисел - числа нуль и отрицательных чисел. Множество целых чисел обозначают как Z.

Натуральные числа - $1,2, \ldots, n, \ldots$

Натуральные числа в множестве целых чисел называются положительными целыми числами.

Множество целых чисел является упорядоченным, то есть для любых двух целых чисел m и n справедливо только одно из следующих соотношений: или m = n, или m > n, или m .

Для положительных чисел n записывают $n>0$, для отрицательных - $n \lt 0$. Если надо указать, что число может быть положительным или нулем, то пишут $n \geq 0$ и говорят, что оно неотрицательное. Аналогично, запись $n \leq 0$ означает, что число n отрицательно или нуль. Такие числа называются неположительными.


Арифметические операции с целыми числами

Определение

Абсолютным значением или модулем числа n называется число, которое обозначается |n| и вычисляется по правилу:

$$|n|=\left\{\begin{array}{l} n, n \geq 0 \\ -n, n \leq 0 \end{array}\right.$$

Модуль числа $n$ положителен как для положительных, так и для отрицательных целых чисел; абсолютное значение равно нулю только в том случае, если $n=0$.

Пример

Задание. Найти абсолютные значения чисел 5 и - 2

Решение. Так как число 5 положительное ($5 > 0$), тогда $|5| = 5$. Из того, что $(-2)$ - отрицательное число, то $|-2| = -(-2) = 2$.

Сложение целых чисел. Для того, чтобы сложить два целых числа с одинаковыми знаками, нужно сложить их модули и перед суммой поставить их общий знак.


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 459 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти сумму $2 + 3; -4 + (-5)$

Решение. $$2+3=+(|2|+|3|)=+(2+3)=+5=5$$

$$-4+(-5)=-(|-4|+|-5|)=-(4+5)=-9$$

Для того, чтобы сложить два целых числа с разными знаками, нужно из модуля большего числа вычесть модуль меньшего и перед результатом поставить знак большего по модулю числа.

Пример

Задание. Вычислить $-7 + 4; -3 + 5$

Решение. $$-7+4=-7+(+4)=-(|-7|-|4|)=-(7-4)=-3$$

$$-3+5=-3+(+5)=+(|5|-|-3|)=+(5-3)=+2=2$$

Вычитание целых чисел. Вычитание целых чисел сводится к сложению уменьшаемого и числа, противоположному вычитаемому.

Пример

Задание. Вычислить $-7 - 3; 6 - (-5)$

Решение. $$6-(-5)=(+6)-(-5)=6+[-(-5)]=6+5=11$$

$$4 \cdot(-5)=+4 \cdot(-5)=-|4| \cdot|-5|=-4 \cdot 5=-20$$

Умножение целых чисел. Для того, чтобы перемножить два целых числа, нужно перемножить их модули и перед произведением поставить знак плюс (+), если исходные числа были одного знака, и минус (-) - если разного.

Пример

Задание. Вычислить $(-15) : 3; 6: (-2); (-20) : (-4)$

Решение. $$4 \cdot(-5)=+4 \cdot(-5)=-|4| \cdot|-5|=-4 \cdot 5=-20$$

$$(-4) \cdot(-5)=+|-4| \cdot|-5|=4 \cdot 5=20$$

$$(-4) \cdot 5=(-4) \cdot(+5)=-|-4| \cdot|5|=-4 \cdot 5=-20$$

При перемножении нескольких сомножителей знак произведения положителен, если число отрицательных сомножителей чётно, и отрицателен, если нечётно.

Деление целых чисел. Для того, чтобы разделить одно целое число на другое, нужно разделить модуль первого числа на модуль второго и поставить перед частным знак плюс, если знаки делимого и делителя одинаковые, и минус, - если разные.

Пример

Задание. Вычислить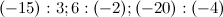

Решение. $$(-15): 3=(-15):(+3)=-|-15|:|3|=-15: 3=-5$$

$$6:(-2)=(+6):(-2)=-|6|:|-2|=-6: 2=-3$$

$$(-20):(-4)=+|-20|:|-4|=20: 4=5$$

Читать следующую тему: рациональные числа.