Содержание:

Формулировка теоремы Герона

Теорема

Площадь треугольника равна корню из произведения разностей полупериметра $p$ треугольника (рис 1) и каждой из его сторон $a$, $b$ и $c$ на полупериметр:

$S=\sqrt{p(p-a)(p-b)(p-c)}$

где полупериметр

$$p=\frac{a+b+c}{2}$$

Треугольник со сторонами $a$, $b$ и $c$.

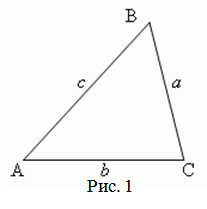
Формула Герона позволяет вычислить площадь треугольника по известным длинам его сторон.

Эта формула содержится в "Метрике" греческого математика и механика Герона Александрийского и названа в его честь. Герон интересовался треугольниками с целочисленными сторонами. Такие треугольники носят название героновых треугольников. Простейшим героновым треугольником является египетский треугольник - прямоугольный треугольник со соотношениями сторон $3 : 4 : 5$ .

Примеры решения задач

Пример

Задание. Вычислите площадь треугольника, зная, что его стороны равны 6 см; 5 см и 2,2 см.

Решение. Полупериметр

$$p=\frac{6+5+2,2}{2}=6,6 (\mathrm{см})$$

Тогда площадь треугольника, согласно формуле Герона, равна:

$$S=\sqrt{6,6 \cdot(6,6-6) \cdot(6,6-5) \cdot(6,6-2,2)}=$$

$$=\sqrt{6,6 \cdot 0,6 \cdot 1,6 \cdot 4,4}=\sqrt{27,8784}=5,28\left(\mathrm{см}^{2}\right)$$

Ответ. $S=5.28\left(\mathrm{см}^{2}\right)$

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 466 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!