Что такое прямоугольный треугольник

Задание. В треугольниках $A B C$, $K L M$ и $D E F$, заданны по два угла:

1) $\angle A=50^{\circ}, \angle B=40^{\circ}$

2) $\angle L=37^{\circ}, \angle M=53^{\circ}$

3) $\angle D=23^{\circ}, \angle E=78^{\circ}$

Определить есть ли среди них прямоугольный треугольник.

Решение. Найдем для каждого треугольника, чему равен третий угол, используя свойство, что в треугольнике сумма всех углов равна $180^{\circ}$:

1) $\angle C=180^{\circ}-\angle A-\angle B \Rightarrow \angle C=180^{\circ}-50^{\circ}-40^{\circ}=90^{\circ}$

2) $\angle K=180^{\circ}-\angle L-\angle M \Rightarrow \angle K=180^{\circ}-37^{\circ}-53^{\circ}=90^{\circ}$

3) $\angle F=180^{\circ}-\angle D-\angle E \Rightarrow \angle F=180^{\circ}-23^{\circ}-78^{\circ}=79^{\circ}$

Так как у треугольников $A B C$ и $K L M$ третий угол прямой ( $\angle C=90^{\circ}$ и $\angle K=90^{\circ}$ ), то эти треугольники прямоугольные.

Ответ. $\Delta A B C$ и $\Delta K I M$ - прямоугольные треугольники.

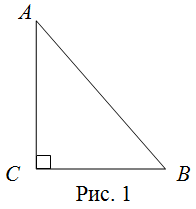
Задание. Дан прямоугольный треугольник $A B C$, $\angle C=90^{\circ}, \angle B=60^{\circ}, A B=6$ см. Найти сторону $B C$.

Решение. В заданном прямоугольном треугольнике сторона $A B$ лежит против прямого угла $C$, то есть является гипотенузой (рис. 1). Стороны $B C$ и $A C$ - катеты. Найдем, чему равен $\angle A$. Так сумма всех углов треугольника равна $180^{\circ}$, то

$$\angle A=180^{\circ}-\angle C-\angle B \Rightarrow \angle A=180^{\circ}-90^{\circ}-60^{\circ}=30^{\circ}$$

Искомая сторона $B C$ является катетом, который лежит против угла $\angle A=30^{\circ}$, поэтому равна половине гипотенузы:

$B C=\frac{1}{2} A B \Rightarrow B C=\frac{6}{2} \Rightarrow B C=3$ (см)

Ответ. $B C=3$ см