Прямоугольник - это параллелограмм, у которого все углы прямые (то есть равны $90^{\circ}$).
Содержание:
Определение прямоугольника
Определение
На рисунке 1 $ABCD$ - прямоугольник, $\angle A=\angle B=\angle C=\angle D=90^{\circ}, A B=C D, B C=A D$.
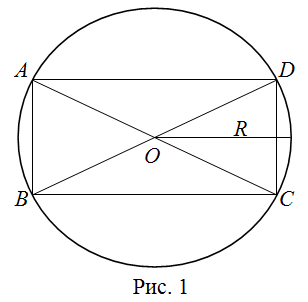
Поскольку прямоугольник является частным случаем параллелограмма, то он обладает всеми свойствами параллелограмма. Кроме этих свойств, прямоугольник имеет присущее только ему свойство - Диагонали прямоугольника равны ($A C=B D$).
Признак прямоугольника
Если диагонали параллелограмма равны, то такой параллелограмм - прямоугольник.
Около любого прямоугольника можно описать окружность. Центром этой окружности будет точка пересечение диагоналей, а радиус будет равен (рис. 1)
$$R=\frac{A C}{2}$$
Примеры решения задач
Пример
Задание. В прямоугольнике $ABCD$ одна сторона на 2 см больше второй. Найти стороны прямоугольника, если его периметр равен 20 см.
Решение. Сделаем рисунок (рис. 2)
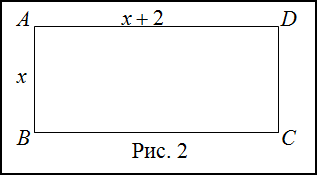
Пусть меньшая сторона прямоугольника равна $x$ см, тогда большая равна $(x+2)$ см. Так как периметр равен $P_{A B C D}=2(A B+A D)=20$, получаем следующее уравнение
$2(x+(x+2))=20$
$x+x+2=20 : 2$
$\quad 2 x=10-2$
$\quad 2 x=8$
$x=4$
Таким образом, $A B=C D=4$ см, $A D=B C=6$ см.
Ответ. $A B=C D=4$ см, $A D=B C=6$ см.
Пример
Задание. Вокруг прямоугольника $ABCD$ со сторонами 12 дм и 5 дм описана окружность радиуса $R$. Найти $R$.
Решение. Сделаем рисунок (рис. 3.)
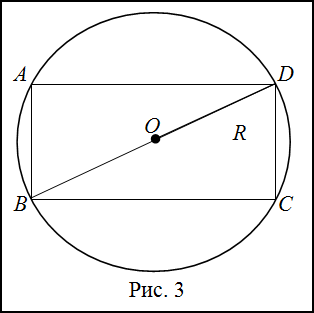
Радиус описанной окружности равен половине диагонали. Найдем диагональ. Рассмотрим $\Delta A B D$, он прямоугольный ( $\angle A=90^{\circ}$). По теореме Пифагора:
$$B D=\sqrt{A B^{2}+A D^{2}}$$
подставляя значение сторон, получим
$B D=\sqrt{12^{2}+5^{2}}$
$B D=\sqrt{144+25}=\sqrt{169}$
$B D=13$ (дм)
Тогда $R=\frac{B D}{2} \Rightarrow R=\frac{13}{2} \Rightarrow R=6,5$ (дм)
Ответ. $R=6,5$ дм
Читать дальше: что такое параллелограмм.










