Формулы квадрата

Содержание:

• Формулы площади квадрата:
• Формулы периметра квадрата:

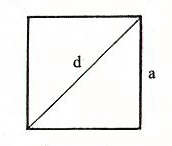
Квадрат — правильный четырёхугольник, у которого все стороны и углы равны между собой. Может быть определён как прямоугольник, у которого две смежные стороны равны между собой, или как ромб, у которого все углы прямые. У квадрата есть две диагонали, соединяющие несмежные вершины.

Формулы площади квадрата:

Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади квадрата выражается числом заключающихся в него квадратных единиц.

1) Площадь квадрата равна квадрату длины его стороны (a).

2) Площадь квадрата равна половине квадрата длины его диагонали (d).

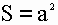
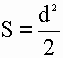
S - площадь квадрата

a - длина стороны квадрата

d - длина диагонали квадрата

См. также: Программа для расчета площади квадрата.

Формулы периметра квадрата:

Периметр геометрической фигуры - суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.

1) Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).

2) Периметр квадрата равен произведению длины его диагонали на два корня из двух.

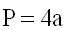
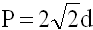
P - периметр квадрата

a - длина стороны квадрата

d - длина диагонали квадрата

См. также: Программа для расчета периметра квадрата.

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 456 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Узнать стоимость