Содержание:

График функции $y=f(x)$, дифференцируемой на интервале $(a ; b)$, является на этом интервале выпуклым, если график этой функции в пределах интервала $(a ; b)$ лежит не выше любой своей касательной (рис. 1).

График функции $y=f(x)$, дифференцируемой на интервале $(a ; b)$, является на этом интервале вогнутым, если график этой функции в пределах интервала $(a ; b)$ лежит не ниже любой своей касательной (рис. 2).

Выпуклость и вогнутость функции

Теоремы о выпуклости функции и точках перегиба

Теорема

(Об условиях выпуклости или вогнутости графика функции)

Пусть функция $y=f(x)$ определена на интервале $(a ; b)$ и имеет непрерывную, не равную нулю в точке $x_{0} \in(a ; b)$ вторую производную. Тогда, если $f^{\prime \prime}(x)>0$ всюду на интервале $(a ; b)$, то функция имеет вогнутость на этом интервале, если $f^{\prime \prime}(x) \lt 0$, то функция имеет выпуклость.

Определение

Точкой перегиба графика функции $y=f(x)$ называется точка $M\left(x_{1} ; f\left(x_{1}\right)\right)$, разделяющая промежутки выпуклости и вогнутости.

Теорема

(О необходимом условии существования точки перегиба)

Если функция $y=f(x)$ имеет перегиб в точке $M\left(x_{1} ; f\left(x_{1}\right)\right)$, то $f^{\prime \prime}\left(x_{1}\right)=0$ или не существует.

Теорема

(О достаточном условии существования точки перегиба)

Если:

  1. первая производная $f^{\prime}(x)$ непрерывна в окрестности точки $x_{1}$;
  2. вторая производная $f^{\prime \prime}(x)=0$ или не существует в точке $x_{1}$;
  3. $f^{\prime \prime}(x)$ при переходе через точку $x_{1}$ меняет свой знак,

тогда в точке $M\left(x_{1} ; f\left(x_{1}\right)\right)$ функция $y=f(x)$ имеет перегиб.

Схема исследования функции на выпуклость, вогнутость

  1. Найти вторую производную функции.
  2. Найти точки, в которых вторая производная равна нулю или не существует.
  3. Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.

Пример

Задание. Найти интервалы выпуклости/вогнутости функции $y=\frac{x^{3}}{6}-x^{2}+3 x+1$

Решение. Найдем вторую производную заданной функции:

$y^{\prime \prime}=\left(\frac{x^{3}}{6}-x^{2}+3 x+1\right)^{\prime \prime}=\left(\frac{x^{2}}{2}-2 x+3\right)^{\prime}=x-2$

Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение $y^{\prime \prime}(x)=0$:

$y^{\prime \prime}(x)=x-2=0 \Rightarrow x=2$

Исследуем знак второй производной слева и справа от полученной точки:

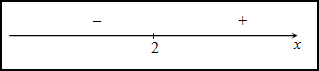
Так как на промежутке $(-\infty ; 2)$ вторая производная $y^{\prime \prime}(x) \lt 0$, то на этом промежутке функция $y(x)$ выпукла; в силу того, что на промежутке $(2 ;+\infty)$ вторая производная $y^{\prime \prime}(x)>0$ - функция вогнута. Так как при переходе через точку $x=2$ вторая производная сменила знак, то эта точка является точкой перегиба графика функции.

Ответ. Точка $x=2$ - точка перегиба графика функции.

На промежутке $(-\infty ; 2)$ функция выпукла, на промежутке $(2 ;+\infty)$ функция вогнута.

Читать дальше: асимптоты графика функции.

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 449 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!