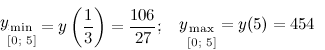Если функция $y=f(x)$ определена и непрерывна на отрезке $[a ; b]$ , то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение $M$ функция $f(x)$ принимает в точке $x_{0} \in[a ; b]$, то $M=f\left(x_{0}\right)$ будет локальным максимумом функции $f(x)$, так как в этом случае существует окрестность точки $x_{0}$, такая, что $f(x) \leq f\left(x_{0}\right)$ .

Однако свое наибольшее значение $M$ функция $f(x)$ может принимать и на концах отрезка $[a ; b]$ . Поэтому, чтобы найти наибольшее значение $M$ непрерывной на отрезке $[a ; b]$ функции $f(x)$, надо найти все максимумы функции на интервале $(a ; b)$ и значения $f(x)$ на концах отрезка $[a ; b]$, то есть $f(a)$ и $f(b)$, и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.

Наименьшим значением $m$ непрерывной на отрезке $[a ; b]$ функции $f(x)$ будет наименьший минимум среди всех минимумов функции $f(x)$ на интервале $(a ; b)$ и значений $f(a)$ и $f(b)$.

Пример

Задание. Найти наибольшее и наименьшее значение функции $y(x)=4 x^{3}-2 x^{2}+4$ на отрезке $[0 ; 5]$ .

Решение. Находим производную функции:

$y^{\prime}(x)=\left(4 x^{3}-2 x^{2}+4\right)^{\prime}=12 x^{2}-4 x$

Находим точки, в которых производная равна нулю:

$y^{\prime}(x)=0 \Rightarrow 12 x^{2}-4 x=0 \Rightarrow x_{1}=0, x_{2}=\frac{1}{3}$

Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку $[0 ; 5]$ . Оба значения лежат в этом промежутке.

Находим значения функции в полученных стационарных точках из промежутка и на концах промежутка:

$y(0)=4 ; \quad y\left(\frac{1}{3}\right)=\frac{106}{27} \approx 3,92 ; y(5)=454$

Таким образом,

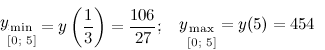
Ответ.

Читать дальше: выпуклость функции, точки перегиба.

Слишком сложно?

Наибольшее и наименьшее значение функции, непрерывной на отрезке не по зубам? Тебе ответит эксперт через 10 минут!

Опиши задание