Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
Содержание:
- Применение первого замечательного предела на практике
- Следствия из первого замечательного предела
- Первый замечательный предел:
Определение
Применение первого замечательного предела на практике
Пример
Задание. Найти предел $\lim _{x \rightarrow 0} \frac{\sin 4 x}{2 x}$
Решение. Воспользуемся заменой и первым замечательным пределом.
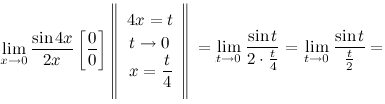
$=\lim _{t \rightarrow 0} \frac{2 \sin t}{t}=2 \lim _{t \rightarrow 0} \frac{\sin t}{t}=2 \cdot 1=2$
Ответ. $\lim _{x \rightarrow 0} \frac{\sin 4 x}{2 x}=2$
Пример
Задание. Найти предел $\lim _{x \rightarrow 0} \frac{\operatorname{tg} x}{5 x}$
Решение. Разложим тангенс на синус и косинус и воспользуемся свойствами пределов.
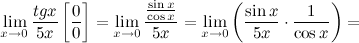
$=\lim _{x \rightarrow 0} \frac{\sin x}{5 x} \cdot \lim _{x \rightarrow 0} \frac{1}{\cos x}=\frac{1}{5} \lim _{x \rightarrow 0} \frac{\sin x}{x} \cdot \frac{\lim _{x \rightarrow 0} 1}{\lim _{x \rightarrow 0} \cos x}=$
$=\frac{1}{5} \cdot 1 \cdot \frac{1}{\cos 0}=\frac{1}{5} \cdot \frac{1}{1}=\frac{1}{5}$
Ответ. $\lim _{x \rightarrow 0} \frac{\operatorname{tg} x}{5 x}=\frac{1}{5}$
Следствия из первого замечательного предела
1 $\lim _{x \rightarrow 0} \frac{\operatorname{tg} x}{x}=1$
2 $\lim _{x \rightarrow 0} \frac{\arcsin x}{x}=1$
3 $\lim _{x \rightarrow 0} \frac{\operatorname{arctg} x}{x}=1$
4 $\lim _{x \rightarrow 0} \frac{1-\cos x}{\frac{x^{2}}{2}}=1$
Читать дальше: второй замечательный предел.










