Задание. Найти модуль вектора $\bar{a}=(-1 ; 1)$
Решение. Для нахождения модуля вектора, заданного на плоскости воспользуемся формулой:
$$|\bar{a}|=\sqrt{a_{x}^{2}+a_{y}^{2}}$$Подставляя в неё координаты заданного вектора, будем иметь:
$$|\bar{a}|=\sqrt{(-1)^{2}+1^{2}}=\sqrt{1+1}=\sqrt{2}$$Ответ. $|\bar{a}|=\sqrt{2}$
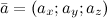 , то его модуль вычисляется по формуле
, то его модуль вычисляется по формуле









