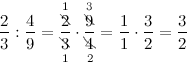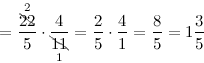Содержание:

Обратная дробь

Если у дроби $\frac{a}{b}$ поменять местами числитель и знаменатель, то получится новая дробь $\frac{b}{a}$ , которая называется обратной дробью к дроби $\frac{a}{b}$

Пример

Задание. Записать дробь, обратную к дроби а) $\frac{2}{3}$ ; б) $\frac{1}{2}$

Решение. Найдем обратные дроби по описанному выше правилу

а) Меняем числитель и знаменатель дроби $\frac{2}{3}$ местами, получаем обратную дробь $\frac{3}{2}$

б) Для нахождения обратной дроби числитель 1 пишем вместо знаменателя, который равен 2, соответственно знаменатель пишем в числитель. В итоге всех преобразований получаем обратную дробь $\frac{2}{1}=2 : 1=2$

Ответ. К дроби $\frac{2}{3}$ обратной является $\frac{3}{2}$, а к $\frac{1}{2}$ - 2

Деление дробей

Чтобы разделить дробь на дробь, нужно первую дробь-делимое оставить без изменений и умножить ее на дробь, обратную ко второй дроби-делителю:

$\frac{a}{b} : \frac{c}{d}=\frac{a}{b} \cdot \frac{d}{c}=\frac{a d}{b c}$


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 446 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти частное от деления дроби  $\frac{2}{3}$  на дробь  $\frac{4}{9}$ 

Решение. Заметим до начала деления, что дробью, обратной к дроби $\frac{4}{9}$ , является дробь $\frac{9}{4}$ . Тогда получаем:

Ответ.   $\frac{2}{3} : \frac{4}{9}=\frac{3}{2}$

Деление смешанных дробей

Чтобы поделить смешанные дроби, их надо записать в виде неправильных дробей и затем делить по правилу деления обыкновенных дробей.

Пример

Задание. Вычислить $4 \frac{2}{5} : 2 \frac{3}{4}$

Решение. Выполним деление смешанных дробей по описанному выше правилу

$4 \frac{2}{5} : 2 \frac{3}{4}=\frac{4 \cdot 5+2}{5} : \frac{2 \cdot 4+3}{4}=\frac{22}{5} : \frac{11}{4}=$

Ответ.   $4 \frac{2}{5} : 2 \frac{3}{4}=1 \frac{3}{5}$

Читать следующую тему: нахождение дроби от числа и наоборот.