Определение

Универсальной тригонометрической подстановкой называется подстановка вида $\operatorname{tg} \frac{x}{2}=t$

В англоязычной литературе в честь выдающегося немецкого математика Карла Вейерштрасса (1815 - 1897) называется подстановкой Вейерштрасса.

Указанная подстановка применяется при интегрировании, когда подынтегральное выражение рационально зависит от тригонометрических функций. Указанная замена позволяет свести интеграл от тригонометрической функции к интегралу от рациональной функции.

При этом следует учесть, что из равенства $\operatorname{tg} \frac{x}{2}=t$ получаем:

$\frac{x}{2}=\operatorname{arctg} t \Rightarrow x=2 \operatorname{arctg} t \Rightarrow$

$d x=\frac{2 d t}{1+t^{2}}, \sin x=\frac{2 \operatorname{tg} \frac{x}{2}}{1+\operatorname{tg}^{2} \frac{x}{2}}=\frac{2 t}{1+t^{2}}$

$\cos x=\frac{1-\operatorname{tg}^{2} \frac{x}{2}}{1+\operatorname{tg}^{2} \frac{x}{2}}=\frac{1-t^{2}}{1+t^{2}}$

Пример

Задание. Найти неопределенный интеграл $\int \frac{d x}{5-\sin x+\cos x}$

Решение. Воспользуемся универсальной тригонометрической подстановкой:

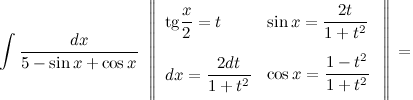
$=\int \frac{\frac{2 d t}{1+t^{2}}}{5-\frac{2 t}{1+t^{2}}+\frac{1-t^{2}}{1+t^{2}}}=2 \int \frac{d t}{5\left(1+t^{2}\right)-2 t+1-t^{2}}=$

$=2 \int \frac{d t}{4 t^{2}-2 t+6}=\int \frac{d t}{2 t^{2}-t+3}=\frac{1}{2} \int \frac{d t}{t^{2}-\frac{t}{2}+\frac{3}{2}}=$

$=\frac{1}{2} \int \frac{d t}{t^{2}-2 t \cdot \frac{1}{4}+\left(\frac{1}{4}\right)^{2}-\left(\frac{1}{4}\right)^{2}+\frac{3}{2}}=\frac{1}{2} \int \frac{d t}{\left(t-\frac{1}{4}\right)^{2}+\frac{23}{16}}=$

$=\frac{1}{2} \int \frac{d t}{\left(t-\frac{1}{4}\right)^{2}+\left(\frac{\sqrt{23}}{4}\right)^{2}}=\frac{1}{2} \cdot \frac{1}{\frac{\sqrt{23}}{4}} \cdot \operatorname{arctg} \frac{t-\frac{1}{4}}{\frac{\sqrt{23}}{4}}+C=$

$=\frac{2 \sqrt{23}}{23} \operatorname{arctg} \frac{\sqrt{23}(4 t-1)}{23}+C=\frac{2 \sqrt{23}}{23} \operatorname{arctg} \frac{\sqrt{23}\left(4 \operatorname{tg} \frac{x}{2}-1\right)}{23}+$

Ответ. $\int \frac{d x}{5-\sin x+\cos x}=\frac{2 \sqrt{23}}{23} \operatorname{arctg} \frac{\sqrt{23}\left(4 \operatorname{tg} \frac{x}{2}-1\right)}{23}+C$

Больше примеров решений Решение интегралов онлайн

Читать первую тему - неопределенный интеграл, раздела интегралы.

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 467 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!