Пусть задан вектор $\overline{A B}$ и некоторая ось $l$ с единичным вектором $\overline{e}$. Точки $A_{1}$ и $B_{1}$ - проекции точек $A$ и $B$ на ось $l$ соответственно.

Определение

Проекцией вектора $\overline{A B}$ на ось $l$ называется длина отрезка $A_{1} B_{1}$, взятая со знаком "+", если направление $\overline{A_{1} B_{1}}$ совпадает с направлением вектора $\overline{e}$, и со знаком "-", если направление $\overline{A_{1} B_{1}}$ противоположно направлению единичного вектора оси $l$ (рис. 1).

Проекция вектора, рисунок

Проекция вектора $\overline{A B}$ на ось $l$ обозначается символом 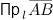Проекция вектора на ось, формула.

Свойства проекции векторов

Проекции равных векторов на одну и туже ось равны.

Вектор $\overline{A B}$ и его проекция - вектор $\overline{A_{1} B_{1}}$ - связаны следующим векторным равенством:

$\overline{A_{1} B_{1}}=\overline{e} \cdot \Pi \mathrm{p}_{l} \overline{A B}$

Проекция вектора $m \overline{a}$ на некоторую ось $l$ равна проекции на эту же ось вектора $\overline{a}$, умноженного на число $m$:

$\Pi \mathrm{p}_{l}(m \overline{a})=m \Pi \mathrm{p}_{l} \overline{a}$

Проекция вектора $\overline{a}$ на ось $l$ равна произведению модуля этого вектора на косинус угла между ним и положительным направлением оси на некоторую ось $l$:

$$\Pi p_{l} \bar{a}=|\bar{a}| \cos (\bar{a} ; l)$$

Читать дальше: правая и левая тройки векторов.

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 453 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!