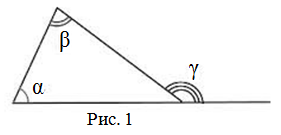
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним:
Содержание:
Формулировка теоремы о внешнем угле треугольника
Теорема
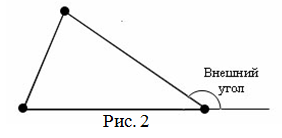
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине (внутренним углом) (рис. 2).
Следствие
Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Примеры решения задач
Пример
Задание. В треугольнике $ABC$ угол $A$ равен $30^{\circ}$, угол $B - 80^{\circ}$. Найти градусную меру угла, смежного с третьим углом треугольника.
Решение. Согласно теореме о внешнем угле треугольника, искомый угол равен сумме углов не смежных с ним, то есть:
$$\alpha=30^{\circ}+80^{\circ}=110^{\circ}$$Ответ. $\alpha=110^{\circ}$
Пример
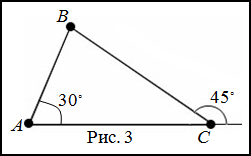
Задание. В треугольнике $ABC$ угол $A$ равен $30^{\circ}$, а внешний угол при вершине $C$ равен $45^{\circ}$. Найти остальные углы треугольника $ABC$ .
Решение. Сделаем чертеж к задаче (рис. 3).
Согласно теореме о внешнем угле треугольника, получаем равенство для нахождения градусной меры угла $B$:
$$45^{\circ}=30^{\circ}+\angle B \Rightarrow \angle B=15^{\circ}$$Угол $C$, как смежный угол, равен
$$\angle C=180^{\circ}-45^{\circ}=135^{\circ}$$Ответ. $\angle B=15^{\circ}, \angle C=135^{\circ}$










