Содержание:

Формула

Чтобы найти площадь равностороннего треугольника (рис. 1), нужно квадрат его стороны умножить на $\sqrt{3}$ и поделить на четыре, то есть

$$\mathrm{S}_{\Delta}=\frac{a^{2} \sqrt{3}}{4}$$

Эту формулу легко получить из общей формулы для площади треугольника

$$\mathrm{S}_{\Delta A B C}=\frac{1}{2} a b \sin \alpha$$

при условии, что $a=b$ (так как треугольник равносторонний) и $\alpha=60^{\circ}$ (угол равностороннего треугольника).

Напомним, что треугольник называется равносторонним, если все его стороны равны.

Примеры вычисления площади равностороннего треугольника

Пример

Задание. Найти площадь равностороннего треугольника $ABC$, если известно, что его сторона равна 2 дм.

Решение. Подставив заданное значение в формулу, будем иметь:

$\mathrm{S}_{\Delta A B C}=\frac{2^{2} \cdot \sqrt{3}}{4}=\frac{4 \cdot \sqrt{3}}{4}=\sqrt{3}$ (дм2)

Ответ. $\mathrm{S}_{\Delta A B C}=\sqrt{3}$ (дм2)

Все формулы площади Калькулятор площади треугольника

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 462 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти площадь равностороннего треугольника $ABC$, если его высота равна 3 м.

Решение. Сделаем чертеж (рис. 2).

Так треугольник равносторонний, то его высота $BH$ является и медианой, а это означает, что $AH=HC$ .

Пусть $HC=x$, тогда $AC=2HC=2x=BC$. Рассмотрим прямоугольный треугольник $BHC$. Записываем для него теорему Пифагора:

$$B C^{2}=B H^{2}+H C^{2}$$ $$(2 x)^{2}=2^{2}+x^{2}$$

Решаем полученное уравнение относительно $x$ :

$4 x^{2}-x^{2}=9 \Rightarrow 3 x^{2}=9 \Rightarrow x^{2}=3 \Rightarrow H C=x=\sqrt{3}$ (м)

Отсюда получаем, что

$A C=2 x=2 \sqrt{3}$ (м)

А тогда искомая площадь

$\mathrm{S}_{\Delta A B C}=\frac{(2 \sqrt{3})^{2} \cdot \sqrt{3}}{4}=\frac{12 \sqrt{3}}{4}=3 \sqrt{3}$ (м2)

Ответ. $\mathrm{S}_{\Delta A B C}=3 \sqrt{3}$ (м2)

Остались вопросы?

Здесь вы найдете ответы.

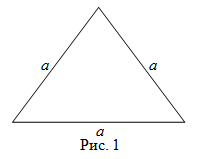
Как можно вычислить площадь равсностороннего треугольника?

Согласно формуле, по которой вычисляется площадь S треугольника с равными сторонами, она равна:

S = √3/4*а, в которой а – это длина стороны фигуры.

Площадь можно также найти следующим образом:

S = a*h/2, где h – это высота.

Высоту можно вычислить, используя теорему Пифагора:

h = а² - (а/2)².

Как можно рассчитать площадь равностороннего треугольника, если известно, что площадь треугольной фигуры, отсекаемой от него средней линией, составляет 6 см. кв.?

Обозначим имеющийся треугольник с равными сторонами как АВС. Обозначим длину стороны как а, и получим, что АВ=ВС=АС=а. Среднюю линию обозначим как МК. Тогда Sмвк = 6 см. кв.

В случае с равносторонним треугольником:

S = а²√3/4

Зная свойство средней линии треугольника, можно записать следующее равенство:

МК = АС/2 = а/2.

В этом случае площадь отсекаемого треугольника равна:

Sмвк = (а/2)²*√3/4 = а²√3/16 см.кв.

В условии дано, что Sмвк = 6 см.кв., тогда:

а²√3/16 = 6

а² = 96/√3.

Площадь равностороннего треугольника:

S = а²√3/4 = (96√3)/(4√3) = 96/4 =24 см.кв.

Как можно вычислить площадь равностороннего треугольника при условии, что его периметр составляет 24 см.?

Найдем сторону равносторонней треугольной фигуры, разделив его периметр на 3:

а = 24:3 = 8 см.

Тогда площадь этой фигуры равна:

S =1/2a²sin 60° = 1/2*64*√3/2 = 16√3 см.кв.

Что представляет собой формула площади равностороннего треугольника?

Обозначив одну из сторон равносторонней треугольной фигуры как а, а высоту, проведенную к ней, - как h, то формула расчета площади этой фигуры будет выглядеть так:

S=ah/2.

Принимая во внимание то, что все стороны данной треугольной фигуры равны, то его высоту можно выразить через сторону и вычислить, используя теорему Пифагора:

h² = а²-(а/2)² = h² = а²- а²/4 = 3а²/4

h = (а√3)/2

Тогда площадь данной фигуры равна:

S = ½ a* h = ½ a*(а√3)/2 = (a²√3)/4

Как выразить длину стороны а из формулы площади равностороннего треугольника?

Для расчета площади треугольника, длины всех сторон которого равны, используется формула:

S=a²√3/4

Перенесем 4 в правую часть равенства:

4S=a²√3.

Тогда:

a² = 4S/√3

а = √4S/√3.

Какая формула используется для вычисления площади равностороннего треугольника с длиной стороны а?

Если известно, что сторона равносторонней треугольной фигуры равна а, то его площадь рассчитывается так:

S = а²√3/4.

Каким образом можно привести доказательство теоремы о площади равностороннего треугольника?

Треугольник имеет два катета – АВ и ВС. Его гипотенуза – ВС. Так как фигура является равносторонней, то АВ = АС.

Требуется доказать, что площадь треугольной фигуры, стороны которой одинаковы, равна произведению длин его катетов, разделенному на два.

Превратим имеющийся треугольник в квадрат, проведя перпендикуляр из его углов, и получим что:

ΔВАС = ΔВСD.

Площадь квадрата равна:

S = а*b.

Диагональ квадрата ВС является гипотенузой треугольника, которая делит квадрат на 2 равные части. Из этого следует, что площадь треугольника равна половине площади квадрата. Что и требовалось доказать.

Как вычислить площадь равностороннего треугольника со стороной длиной 9 см.?

Имеется треугольник АВС с равным сторонами.

ВН = 9 см.

Площадь данной фигуры находится по формуле:

S=1/2*АС*ВН,

в которой АС – основание треугольной фигуре, по длине равное любой из сторон (равносторонний Δ), ВН – высота.

Предположим, что АС = 2а см. Тогда:

АН = АС/2 = ½*2а = а см.

Согласно теореме Пифагора:

АВ² = ВН²+АН².

В данном случае:

(2а)² = 9²+а²

Переносим а² в правую часть уравнения:

4а²-а² = 81

Упрощаем:

3а² = 81.

Отсюда:

а² = 81/3 = 27

а=√27=√9×3=3√3 см.

Теперь можно найти площадь:

S=1/2*9*3√3=1/2*27/√3=27√3/2=13,5√3 см.кв.

Какому числу равна площадь равностороннего треугольника с основанием длиной 6 см.?

Известна формула расчета площади треугольника:

S=1/2*h*b.

Проведем высоту h, которая в равностороннем треугольнике представляет собой также биссектрису и медиану.

Воспользуемся теоремой Пифагора для вычисления высоты:

h = √(36-9) = √27 см.

Тогда:

S = h*3 = 3√27 см.кв.

Возможно ли привести доказательство того, что площадь равностороннего треугольника равна √3*a²/4, в которой длина его стороны обозначена как а?

Доказать, что приведенное в задании утверждение является верным, можно, если превратить имеющуюся треугольную фигуру в параллелограмм/, площадь которого равна произведению длины стороны и высоты.

Параллелограмм состоит из двух треугольников, которые равны. Это значит, что площадь одной из треугольных фигур находится так:

S = a*h /2.

Высоту можно выразить через определение синуса.

Все углы в равносторонней треугольной фигуре равны и составляют 60 градусов (180/3).

sin(60) = V3/2.

Из определения синуса следует:

h/a = sin(60).

Это значит, что:

h = a*V3/2.

Значит:

S = a*a*V3/4.

Почему площадь равностороннего треугольника равна a^2√3/4?

Известно, что площадь любого треугольника можно найти по формуле:

S = 1/2*a*b*sinA,

в которой стороны треугольника обозначены как а и b, а угол, образованный ими, - как А.

Доказано, что каждый угол равносторонней треугольной фигуры составляют 60 градусов (sin60 =sqrt(3)/2), а его стороны имеют одинаковые длины. Если подставить эти значения в формулу, то получим:

S = a22√3/4.

Как найти площадь равностороннего треугольника при условии, что длина каждой его стороны составляет 12 см.?

Площадь треугольника с равными сторонами вычисляется по формуле:

S = √3/4*a².

В данном случае:

S= √3/4*12²= √3*144 /4*1 = 36√3 ≈ 62,35 см.кв.

Согласно формуле Герона:

S = √(р(р-а)(р-a)(p-a))

Для данного треугольника:

Р = 12*3 = 36 см.

Р = р/2 = 36/2 = 18 см.

Тогда:

S = √ (18× (18-12)³) = √(18*6³) = √(18×216)=√3888 ≈ 62,35 см. кв.

Как вычислить площадь правильного равностороннего треугольника, зная радиус круга R?

Площадь треугольника с одинаковыми сторонами считается как:

S = a²√3/4.

Радиус r окружности, которая вписана в данный Δ, равен a√3/6. Значит:

а = 2√3r.

Считаем площадь треугольника:

S = 4*3r²√3/4 = 3√3r².

Радиус R окружности, которая описана около правильной треугольной фигуры, равен a/√3. Следовательно, а = R√3.

В этом случае:

S = R²*3√3/4 = 3√3R²/4.

Известно, что площадь правильного треугольника равна 100√3 м.кв. Как вычислить его сторону?

Площадь треугольника равна:

(a²√3)/4.

В данном случае:

100√3=(a²√3)/4

Тогда:

a²√3=400√3.

Находим а:

a²√3 = 400√3

a² = 400

a = 20 см.

Чему равна площадь правильного треугольника при условии, что диаметр окружности, вписанной в него, = 10 см.?

Если d = 10 см., то r = 10/2 = 5 см.

Известно, что:

r = а√3/6, где а – это длина стороны правильного Δ.

Значит:

5 = а√3/6.

Отсюда:

а = 30/√3 = 10√3 см.

Тогда:

SΔ = a²√3/4 =(10√3)³ *√3/4 = 75√3 см. кв.

Чему равна площадь правильного треугольника со стороной 4 дм.?

Известно, что:

S = 1/2 * a * a sin 60 = 1/2 * 4 * 4 * √3/2 = 4√3 дм.кв.

Площадь также можно найти так:

S = a²√3/4 = 16√3/4 = 4√3 дм.кв.

Как найти площадь правильного треугольника, зная, что длина описанной около него окружности равна 4Пи см.?

Длина окружности через радиус находится так:

L=2πR.

Значит:

R=L/2π=4π/2π=2 у.е.

Имеем правильный треугольник, значит длина его стороны:

a=R*√3=2√3 у.е.

Можем найти SΔ:

S = √3/4a² = √3/43*3 = 3√3 у.е.кв.

Чему равна площадь правильного треугольника и его стороны, если его высота = 14 см.?

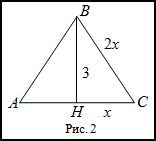
В правильном треугольнике длины всех сторон одинаковы. Это значит, что каждую из них можно обозначить как х. Тогда:

Р (периметр) = х + х + х = 3х см.

Площадь будет равна:

S = 1/2 h * x = 14/2*x = 7х см.кв.

Как найти площадь правильного треугольника с равными сторонами при условии, что радиус круга R?

Площадь треугольной фигуры с равными сторонами считается как:

S = a²√3/4.

Радиус окружности, вписанной в этот Δ, составляет a√3/6. Тогда а = 2√3r.

Находим площадь треугольника:

S = 4*3r²√3/4 = 3√3r².

Радиус R окружности, которая описана около правильного Δ, составляет a/√3. Это означает, что а = R√3.

Теперь можем высчитать площадь треугольника:

S = R²*3√3/4 = 3√3R²/4.

Как найти площадь правильного треугольника при условии, что расстояние от его центра до вершины составляет 2 м.?

Центр правильно треугольной фигуры также является центральной точкой описанной около нее окружности. Ее радиус представляет собой расстояние от центра до вершины фигуры:

а=R√3=2√3

Все углы в правильном треугольнике являются одинаковыми и равны по 60 градусов (180/3).

Площадь треугольной фигуры рассчитывается как:

а²sin60°/2=(2√3)²√3/2/2=6√3 м.кв.

Как найти площадь правильного треугольника, если определено, что сторона имеет длину, аналогичную длине стороны ромба с диагоналями 10 см. и 12 см.?

Предположим, что BD = 10 см., а АС = 12 см.

Диагонали ромба перпендикулярны и делятся на две равные части, пересекаясь в определенной точке.

ΔАВО: ∠АОВ = 90°, АО = АС/2 = 6, ВО = BD/2 = 5.

Согласно теореме Пифагора:

АВ = √(АО² + ВО²) = √(36 + 25) = √41.

Треугольник имеет равные стороны, длина каждой из которых аналогична длине стороны ромба:

а = √41.

Тогда:

SΔ = a²√3/4 = 41√3/4 см.кв.

Как найти площадь правильного треугольника периметром 6 см.?

Если длина стороны правильного треугольника указана, то его площадь вычисляется следующим образом:

S = a²√3/4.

Согласно определению правильного треугольника, длины всех его сторон одинаковые. Исходя из этого можно найти его сторону, разделив периметр на три:

а = 6/3 = 2 см.

Ищем площадь, подставив в равенство значение а:

S = 2²√3/4 = S 4√3/4 = √3 см.кв.

Как найти площадь правильного треугольника при условии, что окружность, которая вписана в него, имеет радиус длиной 4 см.?

Площадь треугольника, имеющего стороны одинаковой длины, может быть рассчитана через длину его стороны без применения формулы радиуса окружности, которая вписана в него. Для данной фигуры верно утверждение о том, что высота, биссектриса и медиана делятся в точке пересечения в отношении 2:1. При схематичном изображении можно увидеть, что треугольная фигура АВС включает 6 треугольников с прямыми углами, которые имеют одинаковый катет (R) и гипотенузу (АО=ВО=СО). Следовательно, площадь треугольника АВС будет представлять собой сумму площадей всех 6 треугольников, формирующих его.

Какова формула вычисления площади равностороннего треугольника со стороной а?

Если сказано, что сторона равносторонней треугольной фигуры равна а, то его площадь можно найти:

S = a²√3/4.

Как определить, чему равна длина стороны треугольника с равными сторонами, зная формулу, по которой вычисляется площадь равностороннего треугольника (S=√3/4 а²) и то, что она равна 9√3см²?

Если S=√3/4 а², то в данном случае S=9√3, что означает: 9√3=√3/4 а².

Выразим а²:

а² = 9√3:√3/4 = 9√3 x 4√3 = 36

а = +-√36 = +- 6.

Так как длина стороны не может быть отрицательным числом, то a = 6 см.

Какой вид имеет формула, которая отражает зависимость площади равностороннего треугольника от длины его сторон?

Доказано, что равносторонний треугольник имеет равные углы по 60 градусов. Также известна формула вычисления площади данной фигуры путем умножения длин двух его сторон и синуса угла, который они образуют:

S = 1/2*a*a*sin 60 = a²√3/4 см.кв.

Чему равна площадь равностороннего треугольника и длина его медианы, если известно, что его сторона составляет а?

Если указано, что длина стороны равностороннего треугольника составляет а, то его площадь равна:

S=a²√3/4.

Медиана, проведенная в треугольнике с равными сторонами, также представляет собой его биссектрису и высоту. Из этого следует, что:

h=a√3/2.

Ответ: Площадь треугольника = a²√3/4 см.кв., его медиана = a√3/2 см.

Как определить площадь равностороннего треугольника со стороной, длина которой составляет 8√2 см?

В случае с треугольником с равными сторонами, высота представляет собой также медиану, делящую на две равные части сторону, на которую она опущена. Если применить в данном случае теорему Пифагора, то высота равна:

h = √((8√2)²-(4√2)²)=4√6 см.

Теперь есть возможность найти площадь:

S = (1/2)*8√2*4√6 = 32√3 см. кв.

Площадь также можно найти по формуле для треугольника с равными сторонами:

S =(√3/4)*a² или S =(√3/4)*128 = 32√3 см. кв.

Дано два равносторонних треугольника, площадь одного из которых превышает площадь другого в три раза. Чему будет равна сторона второго равностороннего треугольника, при условии, что сторона первого из них составляет 1 см.?

Для расчета площади треугольника с равными сторонами есть формула:

S = a²√3/4.

Найдем площадь меньшего из треугольников, подставив значение а:

S₁ = 12 √3/4 = √3/4 см.кв.

Известно, что площадь второго треугольника больше площади первой фигуры в три раза. Тогда:

S₂ = 3√3/4.

Очевидно, что сторона большего треугольника составляет √3 см.

Сторона равностороннего треугольника равна 14 см. Чему будет равна его площадь, умноженная на √3?

Формула площади для треугольника с равными сторонами:

S = а²*√3/4.

Подставляем значение а:

S = 14²*√3/4 = 49√3 см. кв.

Умножаем полученное число на √3:

49√3*√3 = 49*3 = 147 см.

Читать дальше: как найти площадь круга.