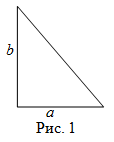Содержание:

Формула

Чтобы найти площадь прямоугольного треугольника $ABC$ (рис. 1), надо найти произведение катетов $a$ и $b$ и поделить его на два. То есть

$$\mathrm{S}_{\Delta A B C}=\frac{a b}{2}$$

Напомним, что катетами прямоугольного треугольника называются стороны, которые пересекаются под прямым углом.

Примеры вычисления площади прямоугольного треугольника

Пример

Задание. Найти площадь прямоугольного треугольника $ABC$, если известно, что длины его катетов равны 3 см и 4 см.

Решение. Искомая площадь равна половине произведения катетов, то есть

$\mathrm{S}_{\Delta A B C}=\frac{3 \cdot 4}{2}=\frac{12}{2}=6$ (см2)

Ответ. $\mathrm{S}_{\Delta A B C}=6$ (см2)

Все формулы площади Калькулятор площади треугольника

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 472 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Вычислить площадь прямоугольного треугольника, один из катетов которого равен 6 см, а гипотенуза 10 см.

Решение. Искомая площадь равна половине произведения катетов. Используя теорему Пифагора, найдем второй катет заданного треугольника:

$b=\sqrt{10^{2}-6^{2}}=\sqrt{100-36}=\sqrt{64}=8$ (см)

Тогда площадь

$S=\frac{6 \cdot 8}{2}=\frac{48}{2}=24$ (см2)

Ответ. $S=24$ (см2)

Читать дальше: как найти площадь равнобедренного треугольника.