Содержание:

Формула

Чтобы найти площадь равнобедренного треугольника (рис. 1), необходимо вычислить произведение половины основания этого треугольника на его высоту:

$$\mathrm{S}_{\Delta}=\frac{1}{2} a h_{a}$$

Напомним, что треугольник называется равнобедренным, если его две стороны равны. Равные стороны называются боковыми сторонами рассматриваемого треугольника, а третья сторона - основанием.

Примеры вычисления площади равнобедренного треугольника

Пример

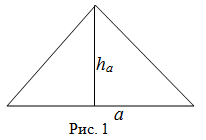
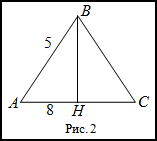
Задание. Найти площадь равнобедренного треугольника $ABC$, если известно, что его основание равно 4 м, а высота, проведенная к этому основанию - 6 м.

Решение. Искомая площадь равна произведению высоты на основание, деленному на два:

$\mathrm{S}_{\Delta A B C}=\frac{4 \cdot 6}{2}=\frac{24}{2}=12$ (м2)

Ответ. $\mathrm{S}_{\Delta A B C}=12$ (м2)

Все формулы площади Калькулятор площади треугольника

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 451 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти площадь равнобедренного треугольника, боковая сторона которого равна 5 см, а основание 8 см.

Решение. Сделаем чертеж (рис. 2).

Проведем высоту $BH$. По свойству равнобедренного треугольника она является и медианой. Поэтому

$A H=H C=\frac{8}{2}=4$ (см)

Рассмотрим прямоугольный треугольник $ABH$. По теореме Пифагора найдем его катет $BH$ :

$B H=\sqrt{A B^{2}-A H^{2}}=\sqrt{5^{2}-4^{2}}=\sqrt{25-16}=\sqrt{9}=3$ (cм)

А тогда искомая площадь

$\mathrm{S}_{\Delta A B C}=\frac{1}{2} A C \cdot B H=\frac{8 \cdot 3}{2}=4 \cdot 3=12$ (см2)

Ответ. $\mathrm{S}_{\Delta A B C}=12$ (см2)

Остались вопросы?

Здесь вы найдете ответы.

Площадь равнобедренного треугольника с прямым углом составляет 16 см кв. Каким образом можно вычислить длину гипотенузы данной треугольной фигуры?

Обозначим через х катет имеющегося равнобедренного треугольника, имеющего прямой угол. В этом случае его площадь будет представлять собой ½ длины его катета, возведенную в квадратную степень. Это значит, что квадрат катета равен двум площадям треугольника (2S). В нашем случае это:

2S = 2*16 = 32 см кв.

Для того чтобы найти длину катета, нужно извлечь корень квадратный из числа 32:

х = 4*√2 см.

Теперь можно высчитать длину гипотенузы, которая будет равна:

х / sin45 = 8 см.

Ответ: Длина гипотенузы равна 8 см.

Имеется равнобедренный треугольник площадью 192 см кв. Его основание составляет 32 см. Как можно вычислить периметр данной треугольной фигуры?

Дан треугольник АВС, в котором АВ=ВС и АС=32 см.

Проведем к основанию треугольника высоту ВН, также являющуюся медианой.

Площадь треугольника равна половине произведения длины его основания на высоту:

S=АС*ВН/2

Из этой формулы можно выразить ВН:

ВН=2S/АС=2*192/32=12 см.

Известно, что в равнобедренном треугольнике две стороны равны:

АВ=ВС=√(ВН²+(АС/2)²)=√(144+256)=20 см.

Теперь можно высчитать периметр (Р) треугольника АВС, который будет равен сумме длин его сторон:

Р=2АВ+АС=40+32=72 см.

Ответ: Периметр равнобедренного треугольника АВС равен 72 см.

Длина гипотенузы равнобедренного треугольника, имеющего прямой угол, составляет 12 см. Как найти площадь данного треугольника?

Обозначим буквой х катет имеющегося треугольника. Тогда по теореме Пифагора:

12²=x² + x², что равно 144=2х²

Отсюда находим значение х:

x²=72, x=√72

Зная длину катета равнобедренного треугольника, можно найти его площадь (S):

S = √72 * √72/2 = 36 см кв.

Ответ: Площадь треугольника равна 36 см кв.

Дан равнобедренный треугольник, угол в основании которого составляет 25 градусов. Площадь данной фигуры равна 16 см кв. Есть еще один равнобедренный треугольник с углом 130 градусов и площадью 4з см кв. Чему будет равно отношение оснований этих двух треугольных фигур?

Разберемся с первым из треугольников. Так как он является равнобедренным, то оба угла при его основании будут равны. Зная о том, что сумма всех углов треугольника равна 180 градусом, мы можем найти третий угол треугольника, находящийся при его вершине:

180-25-25=130 градусов.

Переходим ко второму треугольнику. Известно, что угол при его вершине равен 230 градусом. Исходя из этого можно рассчитать величины его углов, расположенных в основании фигуры:

(180-130)/2=25 градусов.

Очевидно, что треугольники являются подобными на основании равенства углов.

Следует определить коэффициент подобия двух треугольных фигур. Квадрат коэффициента подобия будет равен отношению площадей треугольников:

49/16=kˆ2

Отсюда выражаем k:

k=7/4

Коэффициент подобия представляет собой отношение основания первой подобной треугольной фигуры ко второй. Это значит, что:

С/c=k = 7/4

Ответ: Отношение оснований двух треугольников равно 7/4.

Чему равна площадь равнобедренного треугольника с прямым углом при условии, что длина его гипотенузы составляет с?

Площадь (S) треугольника с прямым углом составляет ½ часть произведения его катетов. Принимая во внимание тот факт, что треугольник является равнобедренным, можно утверждать, что длины его катетов равны. Их можно обозначить через х. В этом случае формулу для расчета площади треугольника можно записать в следующем виде:

S=½x*x=½x²

Согласно теореме Пифагора, действительной для прямоугольного треугольника:

с²=х²+х²=2x²

x²=½c²

Подставим в формулу площади получившееся равенство:

S=½*½с²=¼с² см.кв.

Ответ: Площадь равнобедренного треугольника равна ¼с² см кв.

Как можно рассчитать площадь равнобедренного треугольника, если длина его высоты и основания – величины известные?

Площадь (S) любой треугольной фигуры рассчитывается путем деления пополам произведения длины его основания (с) и высоты (h):

S = ½ c*h

Как найти площадь равнобедренного треугольника?

Площадь каждого треугольника, в том числе и равнобедренного, рассчитывается как половина, взятая от произведения длины высоты треугольника и его основания. Формула имеет следующий вид:

S=1/2 *a*h

Пусть а = 150 см.

Проводим высоту к основанию треугольника. Она же будет являться и медианой по той причине, что треугольник равнобедренный. В результате образовался треугольник с прямым углом и гипотенузой, длина которой равна 85 см. Один из катетов треугольника равен h, а второй рассчитывается как а/2:

150/2=75 см.

Теперь можно рассчитать длину второго катета (на основании теоремы Пифагора):

h=√85²-75²=√7225-5625=√1600=40 см.

Когда все необходимые для расчета площади треугольника величины известны, можно найти ее значение:

S=1/2 *a*h=1/2 *150*40=3000 см.

Как можно найти площадь треугольника при условии, что он является равнобедренным, и его периметр равен 100 см, а основание – 48 см?

Вычислим длину боковой стороны равнобедренного треугольника, отняв от его периметра длину основания и разделив полученное число на 2:

(100-48):2=26 см.

Тогда площадь равнобедренного треугольника с заданными параметрами будет равна:

S=b/4*√(4a²-b²)=12*√(2704-2304)=12*20=240 cм кв.

Чему равна площадь равнобедренного треугольника, длины сторон которого составляют 10 см и 12 см (сумма длин его катетов)?

К основанию равнобедренного треугольника проведем высоту, делящую его на две равные треугольные фигуры, каждая из которых имеет угол 90 градусов и катет длиной 12/2 = 6 см. Гипотенуза подобных треугольников имеет длину 10 см.

В случае с прямоугольным треугольником может быть применима теорема Пифагора, которая поможет найти катет, являющийся высотой треугольника:

h² = 10² - 6² = 64 см

Избавимся от квадратов:

h = 8 см.

Тогда площадь треугольника будет равна:

S = 12 * 8 : 2 = 48 см кв.

Как рассчитать площадь равнобедренного треугольника, если известно о том, что длина его гипотенузы составляет 44 см?

Введем условные обозначения, согласно которым х – это длина одного из катетов равнобедренного треугольника. В этом случае длина второго катета тоже будет равна х. Зная длину гипотенузы, можно записать формулу теоремы Пифагора для имеющегося треугольника:

х²+ х² = 44²

2х² = 1936

Отсюда можем найти значение х:

x=√968

Найдя длину катета равнобедренного треугольника, можно вычислить его площадь (S), равную ½ произведения длин его катетов:

S = √968*√968/2 = 484 см кв.

Каким образом возможно высчитать площадь равнобедренного треугольника через стороны и длину его основания?

Располагая сведениями о длине основания (b) и стороны (a) треугольной фигуры с равными катетами, возможно рассчитать площадь (S) этой фигуры. С этой целью следует пользоваться приведенной ниже формулой:

S = b/4×√ 4× a²-b².

Возможно ли определить площадь равнобедренного треугольника через его боковые стороны и образованный ими угол?

Информация о длине боковых сторон (а) треугольной фигуры с катетами равной длины и размере угла (α), который образован этими катетами, позволит определить площадь этой фигуры. В этом поможет следующая формула:

S = 1/2a2 * sin(α).

Как можно высчитать площадь равнобедренного треугольника при условии, что известна длина его основания и угол?

Для расчета площади треугольной фигуры с катетами равной длины, при условии, что известна их длина (а), основание (b) и угол, который образован основанием и одним из катетов(α), используется следующая формула:

S = ½ * a * b * sin(α)

Длина основания равнобедренного треугольника превышает длину его боковой стороны на 3 см. Периметр данной треугольной фигуры равен 30 см. Как можно высчитать длину основания данного равнобедренного треугольника?

Примем неизвестную длину основания равнобедренного треугольника за х. В данном случае длина каждой из боковых сторон, которые в равнобедренном треугольнике равны, будет составлять (х-3). Известно, что периметр (Р) треугольника равен 30 см. Тогда:

Р = 3х-6 = 30 см.

Отсюда можно вывести х:

х = (30+6)/3 = 12 см.

Ответ: Длина основания равна 12 см.

Высота, проведенная в равнобедренном треугольнике, равна 15 см. Длина основания данной фигуры превышает длину его боковой стороны на 15 см. Как найти основание равнобедренного треугольника в этом случае?

Примем х за длину основания равнобедренного треугольника. Тогда длина его боковой стороны будет составлять (х-15). Высота, проведенная в треугольнике с прямым углом, также представляет собой его медиану, которая делит его на две равных треугольных фигуры. Следует рассмотреть одну из образовавшихся треугольных фигур. Для начала вычислим ее основания, используя теорему Пифагора:

с2 = а2 + b2 = (15)²+(0,5x)²=(x-15)²

Из этого получается:

225-x²-30x+225-0,25x²

0=0,75x²-30x

x(0,75x-30)=0

x¹=0 см.

x=40 см.

Очевидно, что сторона треугольной фигуры не может иметь длину, равную 0см. Поэтому можно сделать вывод о том, что ее длина составляет 40 см.

По какой формуле можно высчитать площадь равнобедренного треугольника?

Для ответа на поставленный вопрос следует провести высоту из вершины того угла равнобедренного треугольника, который является противоположным его основанию. После этого длину проведенной высоты (а) нужно умножить на длину основания фигуры (b), а затем разделить полученное значение на два. Формула расчета площади треугольной фигуры, которая является равнобедренной, выглядит следующим образом:

S=a*b/2, или S=1/2a* b.

В равнобедренном треугольнике к его основанию проведена высота, длина которой равна 1,2 см. Длина самого основания фигуры составляет 3,2 см. Как рассчитать длину боковой стороны этого равнобедренного треугольника?

Вычислим половину длины основания данного равнобедренного треугольника:

3,2/2 = 1,6 см.

Имеется треугольник с прямым углом и катетами, длины которых равны 1,2 см и 1,6 см. Требуется определить длину его гипотенузы. Ее можно вычислить, используя теорему Пифагора:

с²=а²+в²

с² = 1,2² + 1,6² = 1,44 + 2,56 = 4

Осталось только извлечь корень квадратный из 4:

с=√4=2 см.

Ответ: Длина боковой стороны равнобедренного треугольника равна 2 см.

Один из углов равнобедренного треугольника является тупым. Одна сторона данной фигуры составляет 14 см, а другая – 8 см. Чему равно основание треугольника с двумя равными сторонами?

Известно, что углы, расположенные у основания равнобедренного треугольника, всегда являются острыми, иначе сумма всех трех углов превышала бы 180 градусов. Исходя из этого, можно сделать вывод о том, что тупой угол расположен у вершины данной треугольной фигуры.

Доказанным фактом является то, что та сторона фигуры, которая расположена напротив тупого угла, имеет большую длину, чем сторона, лежащая против острого угла треугольника. Это позволяет утверждать, что длина основания данного треугольника больше длины его боковой стороны. По причине того, что треугольная фигура является равнобедренной, и известны длины двух ее сторон (8 см и 14 см), можно говорить о том, что неизвестная сторона будет составлять 8 см или 14 см. Если предположить, что длина неизвестной стороны равна 14 см, тогда длина основания будет составлять 8 см, что невозможно, так как противоречит утверждению о расположении больших сторон напротив тупых углов. Это означает, что длина третьей стороны треугольника равна 8 см, а основание в данном случае составляет 14 см.

Равнобедренный треугольник имеет сторону длиной 29 см. Высота, проведенная в нем, составляет 21 см. Чему равно основание треугольника с указанными параметрами?

Для решения данной задачи следует воспользоваться теоремой Пифагора:

с²=а²+в²

Отсюда можно выразить квадрат длины неизвестной стороны, который будет равен разности квадратов известной стороны и высоты:

29²-21² = 400.

Для того чтобы узнать длину основания равнобедренного треугольника, нужно извлечь корень квадратный из числа 400, а затем умножить полученное число на 2:

√400*2 = 20*2 = 40 см.

Ответ: Длина основания равнобедренного треугольника равна 40 см.

Читать дальше: как найти площадь равностороннего треугольника.