Содержание:

С вычислением производной мы сталкиваемся всякий раз, когда требуется определить скорость изменения одной величины - функции в зависимости от изменения другой величины - независимой переменной.

Определение

Средней скоростью изменения функции $y=f(x)$ при переходе независимой переменной от значения $x$ к значению $x+\Delta x$ называется отношение приращения $\Delta y$ функции к приращению $\Delta x$ независимой переменной, то есть

$$V_{c p}=\frac{\Delta y}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{\Delta x}$$

Определение

Истинной или мгновенной скоростью изменения функции $y=f(x)$ при заданном значении независимой переменной $x$ называется предел, к которому стремится средняя скорость изменения функции при стремлению к нулю приращения аргумента $\Delta x$:

$$V=\lim _{\Delta x \rightarrow 0} V_{c p}=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}=f^{\prime}(x)$$

Механический смысл производной

Теорема

(Механический смысл производной)

Пусть задан путь $s=f(x)$ движения материальной точки. Скорость данной материальной точки в момент времени $t$ есть производная от пути $s$ по времени $t$:

$$v(t)=s^{\prime}(t)$$

Пример

Задание. Тело движется прямолинейно по закону $s(t)=\frac{2}{3} t^{3}-2 t^{2}+4 t$ (м). Определить скорость его движения в момент $t=10$ с.

Решение. Искомая скорость - это производная от пути, то есть

$$\begin{array}{l} v(t)=s^{\prime}(t)=\left(\frac{2}{3} t^{3}-2 t^{2}+4 t\right)^{\prime}=\left(\frac{2}{3} t^{3}\right)^{\prime}-\left(2 t^{2}\right)^{\prime}+(4 t)^{\prime}= \\ =\frac{2}{3}\left(t^{3}\right)^{\prime}-2\left(t^{2}\right)^{\prime}+4(t)^{\prime}=\frac{2}{3} \cdot 3 t^{2}-2 \cdot 2 t+4 \cdot 1=2 t^{2}-4 t+4 \end{array}$$

В заданный момент времени

$v(10)=2 \cdot 10^{2}-4 \cdot 10+4=200-40+4=164$ (м/с).

Ответ. $v(10)=164$ (м/с).

Больше примеров решений Решение производных онлайн

Геометрический смысл производной

Производная функции $y=f(x)$, вычисленная при заданном значении $x$, равна тангенсу угла, образованного положительным направлением оси $O_{x}$ и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой $x$:

$$f^{\prime}(x)=\operatorname{tg} \alpha$$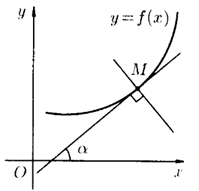

Замечание

Геометрически производная представляет собой угловой коэффициент касательной к графику функции $y=f(x)$ в точке $x_0$ .


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 461 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

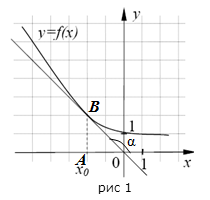
Задание. На рисунке №1 изображен график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$ . Найти значение $f^{\prime}\left(x_{0}\right)$.

Решение. Из геометрического смысла производной получаем, что

$$f^{\prime}\left(x_{0}\right)=\operatorname{tg} \alpha$$

Найдем угол $\alpha$. Рассмотрим треугольник $AOB$ - прямоугольный, равнобедренный. Тогда $$\angle A O B=45^{\circ}$$, а значит

$$\alpha=180^{\circ}-45^{\circ}=135^{\circ}$$

А отсюда следует, что

$$f^{\prime}\left(x_{0}\right)=\operatorname{tg} 135^{\circ}=-1$$

Ответ. $$f^{\prime}\left(x_{0}\right)=-1$$

Больше примеров решений Решение производных онлайн

Читать дальше: геометрическое применение производной: уравнения касательной и нормали, угол между кривыми.