Содержание:

Формулировка теоремы Менелая

Теорема

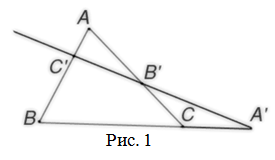
Пусть прямая пересекает треугольник $ABC$, причем $C^{\prime}$ - это точка ее пересечения со стороной $AB$, $A^{\prime}$ - точка ее пересечения со стороной $BC$ и $B^{\prime}$ - точка ее пересечения с продолжением стороны $AC$ (рис. 1). Тогда имеет место соотношение:

$$\frac{A C^{\prime}}{C^{\prime} B} \cdot \frac{B A^{\prime}}{A^{\prime} C} \cdot \frac{C B^{\prime}}{B^{\prime} A}=1$$

Следствия из теоремы Менелая

  1. Тригонометрический эквивалент:

    $$\frac{\sin \angle B A A^{\prime}}{\sin \angle A^{\prime} A C} \cdot \frac{\sin \angle C B B^{\prime}}{\sin \angle B^{\prime} B A} \cdot \frac{\sin \angle A C C^{\prime}}{\sin \angle C^{\prime} C B}=-1$$

    где все углы являются ориентированными.

  2. В сферической геометрии теорема Менелая приобретает вид

    $$\frac{\sin \left|A B^{\prime}\right|}{\sin \left|B^{\prime} C\right|} \cdot \frac{\sin \left|C A^{\prime}\right|}{\sin \left|A^{\prime} B\right|} \cdot \frac{\sin \left|B C^{\prime}\right|}{\sin \left|C^{\prime} A\right|}=1$$

  3. В геометрии Лобачевского теорема Менелая приобретает вид

    $\frac{\operatorname{sh}\left|A B^{\prime}\right|}{\operatorname{sh}\left|B^{\prime} C\right|} \cdot \frac{\operatorname{sh}\left|C A^{\prime}\right|}{\operatorname{sh}\left|A^{\prime} B\right|} \cdot \frac{\operatorname{sh}\left|B C^{\prime}\right|}{\operatorname{sh}\left|C^{\prime} A\right|}=1$

Примеры решения задач

Пример

Задание. В треугольнике $ABC$ на стороне $BC$ взята точка $N$ так, что $NC = 3BN$; на продолжении стороны $AC$ за точку $A$ взята точка $M$ так, что $MA = AC$. Прямая $MN$ пересекает сторону $AB$ в точке $F$. Найти отношение $\frac{BF}{FA}$ .

Решение. Сделаем чертеж к задаче (рис. 2)

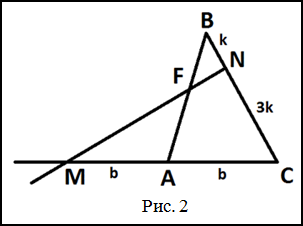
По условию задачи $MA = AC$, $NC = 3BN$. Пусть $MA = AC = b$, $BN = k$,

тогда

$$NC = 3k$$

Прямая $MN$ пересекает две стороны треугольника $ABC$ и продолжение третьей.

Согласно теореме Менелая имеем:

$\frac{C N}{N B} \cdot \frac{B F}{F A} \cdot \frac{A M}{M C}=1$   или  $\frac{3 k}{k} \cdot \frac{B F}{F A} \cdot \frac{b}{2 b}=1$

Отсюда получаем, что

$$\frac{3}{2} \cdot \frac{B F}{F A} \Rightarrow \frac{B F}{F A}=\frac{2}{3}$$

Ответ.  $\frac{B F}{F A}=\frac{2}{3}$


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 450 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. На стороне $PQ$ треугольника $PQR$ взята точка $N$, а на стороне $PR$ - точка $L$, причем $NQ=LR$. Точка пересечения отрезков $QL$ и $NR$ делит отрезок $QL$ в отношении $m : n$, считая от точки $Q$. Найдите отношение $\frac{PN}{PR}$ .

Решение. Сделаем чертеж к задаче (рис. 3)

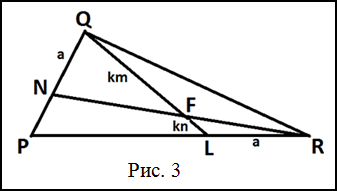
По условию $NQ=LR$, $\frac{Q F}{F L}=\frac{m}{n}$ .

Пусть $NA = LR = a$, $QF = km$, $LF = kn$. Прямая $NR$ пересекает две стороны треугольника $PQR$ и продолжение третьей. Тогда по теореме Менелая

$$\frac{P N}{N Q} \cdot \frac{Q F}{F L} \cdot \frac{L R}{R P}=1 \Leftrightarrow \frac{P N}{a} \cdot \frac{k m}{k n} \cdot \frac{a}{R P}=1 \Rightarrow \frac{P N}{R P}=\frac{n}{m}$$

Ответ.  $\frac{P N}{R P}=\frac{n}{m}$

Историческая справка

Теорема Менелая - это классическая теорема аффинной геометрии. Эта теорема доказывается в третьей книге "Сферики" древнегреческого математика и астронома Менелая Александрийского (ок. 100 г. н.э.). Менелай сначала доказывает теорему для плоского случая, а потом центральным проектированием переносит её на сферу. Возможно, что плоский случай теоремы рассматривался ранее в несохранившихся "Поризмах" Евклида.

Сферическая теорема Менелая была основным средством, с помощью которого решались разнообразные прикладные задачи позднеантичной и средневековой астрономии и геодезии. Ей посвящён ряд сочинений под названием "Книга о фигуре секущих", составленных такими математиками средневекового Востока, как Сабит ибн Кора (836 - 901, астроном, математик, механик и врач), ан-Насави (1010 - 1075, газневидский математик и астроном), ал-Магриби (1220 - 1283, математик и астроном государства Хулагу), Абу Саид ибн Мухаммад ибн Абд-ал-Джалил ас-Сиджизи (951 - 1024, газневидский математик и астроном), Хусам ад-Дин Али ибн Фадлаллах ас-Салар аш-Шами (ум. 1262, среднеазиатский математик и астроном Хорезшахов), Абу Мухаммад Джабир ибн Афлах ал-Ишбили (первая половина 12 в., западноарабский математик и астроном), Абу Джафар Мухаммад ибн Мухаммад Насир ад-Дин ат-Туси (1201 - 1274, персидский математик, механик и астроном).

Итальянский математик и инжинер Джованни Чева (1647 - 1734) в 1678 году предложил доказательство теоремы Менелая и родственной ей теоремы Чевы для плоского случая, основанное на рассмотрении центра тяжести системы из трёх точечных грузов.