Содержание:

Определение кратного числа

Определение

Число $n$ называется кратным некоторому натуральному числу $p$, если оно нацело делится на $p$. При этом говорят что $n$ кратно $p$ .

Некоторые признаки делимости натуральных чисел

  • Признак делимости на 2.

    Число делится на 2, если его последняя цифра есть число четное (то есть 2, 4, 6, 8) или 0.

  • Признак делимости на 3.

    Число делится на 3, если сумма его цифр делится на 3.

  • Признак делимости на 4.

    Число делится на 4, если две его последние цифры - нули или образуют число, делящееся на 4.

  • Признак делимости на 5.

    Число делится на 5, если оно заканчивается либо на 0, либо на 5.

  • Признак делимости на 8.

    Число делится на 8, если три его последние цифры - нули или образуют число, делящееся на 8.

  • Признак делимости на 9.

    Число делится на 9, если сумма его цифр делится на 9.

  • Признак делимости на 11.

    Число делится на 11, если сумма цифр, стоящих на четных местах либо равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на число, делящееся на 11.

  • Признак делимости на 25.

    Число делится на 5, если две его последние цифры - нули или образуют число, делящееся на 25.

Пример

Задание. Среди ниже перечисленных чисел выбрать числа кратные 3:

$$27: 36 ; 58 ; 1119 ; 2345 ; 12354$$

Решение. Будем использовать признак делимости на 3, для этого найдем сумму цифр для каждого числа:

   ;      ;     

   ;     

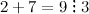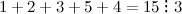
Таким образом, на 3 делятся числа:

$$27 ; 36 ; 1119: 12354$$

Ответ. $27 ; 36 ; 1119: 12354$

Наименьшее общее кратное (НОК)

Определение

Общим кратным нескольких натуральных чисел называется натуральное число, являющееся кратным для каждого из них. Наименьшее из всех кратных называется наименьшим общим кратным (НОК).

Алгоритм нахождения наименьшего общего кратного нескольких чисел:

  1. выписать каноническое разложение данных чисел;
  2. перечислить все простые множители, входящие в канонические разложения данных чисел;
  3. возвести каждый множитель в наибольшую степень, с которой он входит в каноническое разложение данных чисел.

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 456 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти НОК(360; 420)

Решение. Запишем каноническое разложение заданных чисел:

$360 = 2^3 \cdot 3^2 \cdot 5$   и   $420 = 2^2 \cdot 3 \cdot 5 \cdot 7$

Выпишем все простые множители, которые входят в каноническое разложение заданных чисел: $2; 3; 5; 7$ . И возведем их в наибольшую степень, с которой они входят в разложения этих чисел. Получим

НОК(360; 420) $=2^{3} \cdot 3^{2} \cdot 5 \cdot 7=2520$

Ответ. НОК(360; 420) $=2520$

Нахождение НОК онлайн Разложение чисел онлайн

Читать дальше: что такое степень числа.