Если $z=a+b i$, то число $\overline{z}=a-b i$ называется комплексным сопряженным к числу $z$ .
Содержание:
Определение
$\overline{z}=a-b i$
То есть у комплексно сопряженных чисел действительные части равны, а мнимые отличаются знаком.
Например. Комплексно сопряженным к числу $z=2-i$ есть число $\overline{z}=2+i$ .
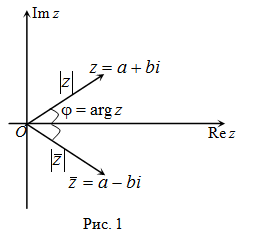
На комплексной плоскости комплексно сопряжённые числа получаются зеркальным отражением друг друга относительно действительной оси.
Свойства комплексно сопряженных чисел
1) Если $z=\overline{z}$, то можно сделать вывод, что рассматриваемое число $z$ является действительным.
Например. $z=2 \in R \Rightarrow \overline{z}=2$ и $z=\overline{z}$
2) Для любого комплексного числа $z$ сумма $z+\overline{z}=2 \operatorname{Re} z$ - действительное число.
Например. Пусть $z=2-3 i$, тогда $\overline{z}=2+3 i$, а тогда
$z+\overline{z}=2-3 i+(2+3 i)=2-3 i+2+3 i=2+2=4 \in R$
3) Для произвольного комплексного числа $z=a+b i$ произведение $z \cdot \overline{z}=|z|^{2} \in R$ .
Например. Пусть $z=2-3 i$, комплексно сопряженное к нему число $\overline{z}=2+3 i$, тогда произведение
$z \cdot \overline{z}=(2-3 i)(2+3 i)=2^{2}-(3 i)^{2}=2^{2}-3^{2} \cdot i^{2}=$
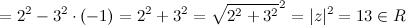
4) Модули комплексно сопряженных чисел равны: $|z|=|\overline{z}|$, а аргументы отличаются знаком (рис. 1).
5) $\overline{z_{1} \pm z_{2}}=\overline{z}_{1} \pm \overline{z}_{2}$
6) $\overline{z_{1} \cdot z_{2}}=\overline{z_{1}} \cdot \overline{z}_{2}$
7) $\frac{\overline{z_{1}}}{z_{2}}=\frac{\overline{z}_{1}}{\overline{z}_{2}}$
8) $\overline{(\overline{z})}=z$
9) Если $z=a+b i$ и $\overline{z}=a-b i$ - комплексно сопряженные числа, то
$a=\operatorname{Re} z=\frac{z+\overline{z}}{2}, b=\operatorname{Im} z=\frac{z-\overline{z}}{2 i}$
Читать дальше: формы записи комплексного числа.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
Статьи по теме
Поможем выполнить
любую работу
