Задание. Найти площадь параллелограмма, если его сторона равна 2 см, а высота, проведенная к этой стороне - 3 см.
Решение. Искомая площадь равна
$S=2 \cdot 3 = 6$ (см2)
Ответ. $S=6$ (см2)
Содержание:
Формулы
Первый способ. Чтобы найти площадь параллелограмма (рис. 1), нужно найти произведение стороны $a$ параллелограмма на высоту $h_a$, проведенную к этой стороне, то есть
$$S=ah_{a}$$
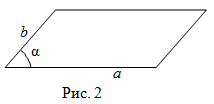
Второй способ. Чтобы найти площадь параллелограмма, надо найти произведение двух его смежных сторон $a$ и $b$, умноженное на синус угла $\alpha$ между ними (рис. 2):
$$\mathrm{S}=a b \sin \alpha$$
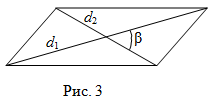
Третий способ. Чтобы найти площадь параллелограмма, надо найти полупроизведение его диагоналей $d_1$ и $d_2$ на синус угла $\beta$ между ними (рис. 3):
$$\mathrm{S}=\frac{1}{2} d_{1} d_{2} \sin \beta$$
Примеры вычисления площади параллелограмма
Пример
Пример
Задание. Найти площадь параллелограмма, одна сторона которого равна 4 см, вторая на 3 см больше и тупой угол параллелограмма равен $120^{\circ}$.
Решение. Найдем вторую сторону параллелограмма:
$b=4+3=7$ (см)
Так как сумма углов параллелограмма, прилежащих к одной стороне, равна $180^{\circ}$, то делаем вывод, что угол между сторонами равен
$$\alpha=180^{\circ}-120^{\circ}=60^{\circ}$$Тогда искомая площадь равна
$\mathrm{S}=4 \cdot 7 \cdot \sin 60^{\circ}=28 \cdot \frac{\sqrt{3}}{2}=14 \sqrt{3}$ (см2)
Ответ. $\mathrm{S}=14 \sqrt{3}$ (см2)
Остались вопросы?
Здесь вы найдете ответы.
Каким образом можно доказать утверждение о том, что площадь параллелограмма
есть число, получаемое в результате умножения длин двух его сторон,
являющихся смежными, и синуса угла, который образуется между ними?
Параллелограмм следует расположить по горизонтали. Обозначим его верхнее основание как АВ, а противоположное ему основание – как CD. Из точек ВЕ и AF проведем перпендикулярные прямые на нижнее основание фигуры. В результате получится прямоугольник ABEF. Площадь образовавшейся прямоугольной фигуры равна площади параллелограмма по той причине, что параллелограмм ABCD и фигура с прямыми углами ABEF являются равносоставленными, о чем свидетельствует равенство треугольников ВEC и DAF.
Площадь (S) прямоугольника представляет собой произведение длин сторон EF и FA, которое, в свою очередь, равно:
CD*AD*sin(CDA)
Именно это и требовалось доказать.
Параллелограмм имеет смежные стороны длиной 26 см и 32 см. Один из углов
данной фигуры равен 150 градусам. Каким способом можно вычислить площадь
параллелограмма?
Обозначим имеющийся параллелограмм как АВСD. Тогда одна его сторона АВ равна 26 см, а другая АD – 32 см. Угол АВС параллелограмма составляет 150 градусов.
Принимая во внимание тот факт, что сумма внутренних односторонних углов параллелограмма равна 180 градусов, можно говорить о том, что его угол ВАD составляет 30 градусов. Проведем высоту ВК, и в итоге получим треугольник АВК с прямым углом. Длина опущенной высоты как катета, расположенного противоположно углу в 30 градусов, равна 13 см. Площадь (S) параллелограмма есть число, полученное в результате умножения длины высоты на длину стороны. Это значит, что:
S (АВСD) = 13 *32 = 416 см кв.
Ответ: Площадь параллелограмма равна 416 см кв.
Прямая АС проведена через середины двух сторон параллелограмма, которые
являются смежными. Данная прямая отсекает от параллелограмма два
треугольника – FMD и АDС. Площадь одного из отсеченных треугольников
составляет 32 см кв. Как высчитать площадь параллелограмма?
Прямая АС представляет собой диагональ биссектрисы. В этом случае образовавшиеся посредством ее проведения треугольники FMD и АDС являются подобными по причине наличия общего угла А и равенства сторон. На основании этого можно говорить о том, что:
SADC=1/2*ab*sin a
SFDM=1/2 *2a*2b sin a
SADC / SFDM= 32/x
1/4=32/x
x=128
Теперь можно рассчитать площадь параллелограмма (S), которая будет равна 2*х:
S = 128*2 = 256 см кв.
Ответ: Площадь параллелограмма равна 256 см кв.
Параллелограмм имеет стороны, длины которых составляют 10 см и 6 см. Данные
стороны образуют угол, равный 150 градусам. Как рассчитать площадь
параллелограмма в этом случае?
Обозначим угол в 150 градусов буквой В. Зная о том, что внутренние односторонние углы параллелограмма в сумме дают 180 градусов, можно вычислить второй угол А. Он будет равен:
∠А = 180-150 = 30 градусов.
Теперь следует провести высоту ВВ1, которая образует треугольник АВВ1, являющийся прямоугольным. Длина ВВ1 будет равна половине длины стороны, равной 6 см:
ВВ1 = 6/2 = 3 см.
Тогда площадь (S) параллелограмма можно рассчитать, умножив длину ВВ1 на 10 см (длина смежной стороны):
S = 3*10 = 30 см кв.
Ответ: Площадь параллелограмма равна 30 см кв.
Проведенные диагонали делят параллелограмм на четыре треугольных фигуры.
Площадь одной из них равна 7 м кв. Каким образом можно найти площадь
параллелограмма?
Обозначим имеющийся параллелограмм как ABCD. Точкой пересечения его диагоналей является точка О. Образованные диагоналями треугольные фигуры ABO, BCO, CDO, DAO являются одинаковыми по площади. Об этом свидетельствует тот факт, что диагонали параллелограмма делятся ровно пополам в точке их пересечения. Свидетельством того, что все четыре треугольника имеют одинаковые площади, выступает равенство синусов смежных углов. Площадь является ½ числа, которое получено в результате умножения длин сторон треугольника и синуса угла, образованного между ними. Параметры, которые отвечают вычислению площадей треугольников, равны, а это означает равенство и самих площадей.
Если площади всех четырех треугольных фигур равны, то площадь самого параллелограмма будет в четыре раза превышать площадь любого из них. Это значит, что площадь (S) параллелограмма может быть вычислена следующим образом:
S = 4*7 = 28 м кв.
Ответ: Площадь параллелограмма равна 28 м кв.
Дан параллелограмм ABCD, на одной из сторон которого АВ поставлена точка М.
Известно, что площадь треугольника MCD составляет 38 см кв. Как найти
площадь параллелограмма?
Площадь (S) параллелограмма рассчитывается путем умножения длины его основания на длину его высоты.
Прямые МС и МD, проведенные из точки М, делят параллелограмм на треугольники. Площадь первого из них вычисляется как:
S₁ = 1/2 * a * h = 38 см кв.
Формула для расчета площади второго треугольника выглядит так:
S₂ = 1/2 * a₁* h
Площадь третьего треугольника можно найти следующим образом:
S₃ = 1/2 *a₃* h,
где а =а₁ + а₂
Теперь через площади образованных треугольников можно вычислить площадь параллелограмма:
S = S₁ + S₂ + S₃ = 1/2 *(a * h +a₁ * h +a₂ * h) = 1/2 * (a * h + h(a₁ + a₂)) = 1/2 * (a * h + a * h) = 2 * 38 = 76 см. кв.
Ответ: Площадь параллелограмма равна 76 см кв.
Длина основания параллелограмма составляет 5 см, а его высота равна 3 см.
Как найти площадь параллелограмма?
Формула расчета площади параллелограмма (S) включает длину его высоты и длину его основания. Данные элементы нужно перемножить, для того чтобы вычислить площадь фигуры:
S = a*h= 5*6=30 см кв.
Ответ: Параллелограмм имеет площадь 30 см кв.
Имеется параллелограмм ABCD. Посередине его стороны АВ поставлена точка Е,
из которой проведена прямая, образующая треугольник CDE площадью 36 см кв.
Каким образом можно найти площадь параллелограмма?
На продолжение стороны CD опустим перпендикуляр ЕН из точки Е. Он представляет собой высоту для параллелограмма ABCD и треугольника CDE.
Известно, что площадь (S) параллелограмма является произведением длины его стороны и высоты, которая на нее опущена. Площадь треугольника представляет собой ½ от числа, которое получилось в результате умножения длины стороны на высоту, опущенную на нее. На основании этого можно сделать вывод о том, что:
S(ABCD) = EH*CD
S(∆CDE) = ½*EH*CD => 2*S(∆CDE) = EH*CD.
Из этого следует, что:
2*S(∆CDE) = S(ABCD) = 2*36 ед² = 72 ед. кв.
Ответ: Площадь параллелограмма составляет 72 кв. ед.
В каком виде представлена формула, которая предназначена для вычисления
площади параллелограмма?
Для получения возможности рассчитать, чему равна площадь (S) параллелограмма, нужно располагать сведениями о длине его основания (а) и высоты (h). В этом случае площадь можно высчитать при помощи следующей формулы:
S = а* h.
Как найти площадь параллелограмма через синус, если известно, что длины его
сторон равны 8 см и 10 см, а синус одного из его углов составляет 0,05?
Формула, которая предназначена для вычисления площади параллелограмма (S) через синус, выглядит следующим образом:
S = a × b × sin A
В данной формуле буквами a и b обозначены стороны параллелограмма, являющиеся смежными, а А означает угол, который образован между этими сторонами.
Доказано, что синусы смежных углов являются равными. Это значит, что синус тупого угла равен синусу острого угла.
Площадь параллелограмма вычисляем следующим образом:
S = 8 × 10 × 0,05 = 4 см кв.
Ответ: Параллелограмм имеет площадь, равную 4 см кв.
Имеется параллелограмм ABCD, в котором опущена высота на его сторону АВ. Ее
длина равна 12 см. При этом длина AD составляет 24 см. Каким образом можно
высчитать значение синуса угла А?
Высота, опущенная на сторону АВ параллелограмма, обозначена как СК. Полученный в результате треугольник КВС имеет прямой угол.
Sin B=АВ/ВС.
В этом случае ВС=AD=24 см. Так, синус угла В равен:
sinВ=12/24=1/2, что соответствует углу 30 градусов.
В параллелограмме проведены диагонали, длины которых равны 5 см и 28 см.
Между ними образован угол, составляющий 30 градусов. Как можно найти площадь
параллелограмма через синус в данном случае?
Площадь любой из четырехугольных фигур может быть вычислена, если известны длины ее диагоналей и синус угла, образованного между ними. Для этого нужно произвести умножение упомянутых величин, а затем разделить полученное число на 2. В случае с параллелограммом, обозначенным как ABCD, площадь рассчитывается по этой же формуле:
S = 1/2 AC*BD*sin∠AOB = ½*28*5*sin30° = 14*5*1/2 = 7*5 = 35 кв. см.
Ответ: Площадь параллелограмма равна 35 см кв.
Представляется ли возможным высчитать площадь параллелограмма при условии,
что длины двух его диагоналей и образованный в месте их пересечения угол
являются известными величинами?
Площадь параллелограмма (S) представляет собой половину числа, полученного после умножения друг на друга длин проведенных в нем диагоналей, которое умножено на синус образовавшегося в итоге их пересечения угла:
S = ½*d 1*d 2*sin α
Возможно ли рассчитать площадь параллелограмма по диагоналям, длины которых
равны 6 см и 4 см? При этом известно, что образованный ими угол является
прямым.
Для определения площади параллелограмма через известные длины проведенных в нем диагоналей применяется приведенная ниже формула:
S = ½*d 1*d 2*sin α,
где диагонали фигуры обозначены как d 1 и d 2, а синус образованного в результате их пересечения угла - sin α.
Подставим в указанное равенство величины, приведенные в задании:
S = 1/2 * 4 см * 6 см * sin 90° = 12 см кв.
Ответ: Площадь параллелограмма, вычисленная через диагонали, равна 12 см кв.
На одной из сторон параллелограмма ABCD, обозначенной как ВС, отмечена точка
М. Чему будет равна площадь параллелограмма при условии, что площадь
треугольника МАD составляет 21 см кв.?
Под площадью параллелограмма (S) понимается величина, полученная в результате умножения длины его стороны (b) на высоту (h), которая опущена к ней. В виде формулы это выглядит следующим образом:
S =b*h
Площадь треугольной фигуры представляет собой ½ числа, полученного произведением длины стороны на высоту, которая к ней проведена:
S=1/2*b*h,
Отсюда получаем, что:
b*h=2Sт=2*21=42 см кв.
Если говорить о треугольнике МАD, то в нем сторона АD представлена в качестве стороны b, как и в случае с параллелограммом. Высота указанного треугольника будет также представлять собой высоту параллелограмма. Это обусловлено тем, что точка М расположена на стороне, которая противоположна стороне ВС. Из этого следует, что площадь параллелограмма равна 42 см кв.
Ответ: Площадь параллелограмма равна 42 см кв.
Параллелограмм ABCD имеет стороны длиной 10 см и 14 см, а также острый угол
в 60 градусов. Каким образом можно вычислить площадь параллелограмма?
В параллелограмме ABCD нужно провести высоту ВН на сторону AD. После этого получается треугольник АВН с углом в 90 градусов. Можно рассчитать, чему равен еще один угол данного треугольника:
АВН = 90-60 = 30
ВН = АВ*sin60 = 10*корень3/2 = 5*корень3
Таким образом, можно узнать, чему будет равна площадь параллелограмма:
S = AD*ВН = 14*5*√3 = 70*√3 см кв.
Ответ: Площадь параллелограмма составляет 70*√3 см кв.
Дан параллелограмм, через середины пары смежных сторон которого проведена
прямая. Она отсекает треугольную фигуру площадью 32 см кв. Чему в данном
случае равна площадь параллелограмма?
АС представляет собой диагональ биссектрисы. В этом случае оба треугольника FMD и ADC являются подобными по той причине, что они имеют общий угол А и их стороны равны. Из этого следует, что:
S ADC = 1/2*ab*sina
S FDM=1/2 *2a*2bsina
Отношение площадей двух треугольников выглядит как:
S ADC / S FDM= 32/x
1/4=32/x
x=128
Теперь можно высчитать площадь параллелограмма:
S = 128*2 = 256 см кв.
Читать дальше: как найти площадь трапеции.
