Равномерное движение по окружности, теория и онлайн калькуляторы
Равномерное движение по окружности
Пусть материальная точка движется по окружности равномерно. Если движение называют равномерным, значит, модуль скорости при перемещении точки является постоянным ($v=const$). Но нельзя сказать, что ускорение точки при этом равно нулю, так как скорость - величина векторная и кроме модуля у нее есть еще направление, а при криволинейном движении, каким является движение по окружности, направление скорости постоянно изменяется. (Мы знаем, что вектор скорости является касательным к траектории, по которой перемещается наша точка, то есть является касательной к окружности в рассматриваемой точке).
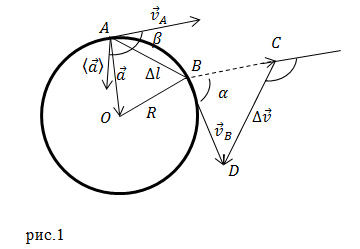
Скорость и ускорение при равномерном движении по окружности
Пусть A и B - точки, принадлежащие траектории движения нашей частицы. При перемещении из точки А в точку В вектор изменения скорости ($\Delta \overline{v}$) равен:
\[\Delta \overline{v}={\overline{v}}_B-{\overline{v}}_A\left(1\right).\]
Устремим время движения частицы к нулю ($\Delta t\to 0$), тогда длина дуги AB будет равна длине хорды AB. Из подобия треугольников AOB и BCD получаем:
\[\frac{\Delta v}{v}=\frac{\Delta l}{R}=\alpha \left(2\right),\]
где $R$ - радиус окружности.
Модуль среднего ускорения точки найдем как:
\[\left\langle a\right\rangle =\frac{\Delta v}{\Delta t}=\frac{v\Delta l}{R\Delta t}\left(3\right).\]
Величину мгновенного ускорения получают при переходе к пределу:
\[a={\mathop{\lim }_{\Delta t\to 0} \left\langle a\right\rangle \ }={\mathop{\lim }_{\Delta t\to 0} \frac{v\Delta l}{R\Delta t}=\frac{v}{r}\ }\mathop{{\rm lim}}_{\Delta t\to 0}\frac{\Delta l}{\Delta t}=\frac{v}{R}v=\frac{v^2}{R}\left(4\right).\]
Выражение (4) говорит нам о том, что при равномерном движении материальной точки по окружности модуль ускорения не изменяется. При этом величина полного ускорения ($a$) совпадает с модулем центростремительного ускорения ($a_n$). Кроме того, можно сказать, что и их направления так же одинаковы. При равномерном движении точки по окружности:
\[\overline{a}={\overline{a}}_n\left(5\right).\]
Вектор среднего ускорения имеет с вектором скорости угол равный$\ \beta $:
\[\beta =\frac{\pi +\alpha }{2}\left(6\right).\]
При $\Delta t\to 0\ $ угол $\alpha \to 0.$ Получаем, что угол между вектором мгновенного ускорения и скорости при равномерном движении по окружности равен $90{}^\circ \ $.
И так, материальная точка, движущаяся с постоянной скоростью по окружности, обладает ускорением, направленным к центру окружности (перпендикулярное вектору скорости), его модуль равен скорости в квадрате, деленной на радиус окружности. Такое ускорение называют центростремительным или нормальным, обозначают его обычно ${\overline{a}}_n$.
\[a_n=\frac{v^2}{R}={\omega }^2R\ \left(7\right),\]
где $\omega $ - угловая скорость движения материальной точки ($v=\omega \cdot R$).
Местоположение точки на окружности можно задавать не только с помощью расстояния от некоторой начальной точки, а так же с помощью угла $\varphi $, поворота радиус-вектора, который определяет положение частицы на траектории (рис.2).
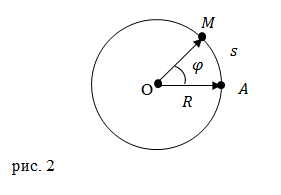
Совместно с углом поворота движение точки по окружности характеризуют при помощи угловой скорости движения ($\omega $), которую определяют как
\[\omega =\frac{d\varphi }{dt}\left(8\right).\]
где $\omega $ характеризует быстроту изменения угла $\varphi $.
При равномерном движении по окружности угловая скорость постоянная величина.
Линейная и угловая скорости движения по окружности связывает формула:
\[v=R\omega \left(9\right).\]
Период и частота при равномерном движении по окружности
Равномерное движение по окружности можно характеризовать при помощи такой физической величины как период обращения
($T$), который определяют как время совершения материальной точкой полного оборота. Используют и частоту ($\nu$) обращения, которую определяют как величину обратную периоду, равную количеству оборотов за единицу времени:
\[\nu =\frac{1}{T}\left(10\right).\]
При равномерном движении по окружности угловая скорость, частота и период связаны как:
\[\omega =\frac{2\pi }{T}=2\pi \nu \left(11\right).\]
Формула (9) дает возможность центростремительное ускорение определить как:
\[a_n=\frac{4{\pi }^2}{T^2}R=4{\pi }^2{\nu }^2R\ \left(12\right).\]
Отметим, что при неравномерном движении по окружности период ($T$) и частота ($\nu$) свой смысл теряют, о них можно говорить только при равномерном движении по окружности.
Примеры задач с решением
Пример 1
Задание: Путь, пройденный точкой по окружности радиуса R, задан уравнением: $s\left(t\right)=At^2+Bt\ (A\ и\ B-постоянные)$. Является ли движение точки равномерным?
Решение: Для ответа на вопрос задачи найдем тангенциальное ускорение материальной точки и сравним его с нулем. При равномерном движении по окружности тангенциальное ускорение частицы должно быть равно нулю. Величину тангенциального ускорения находят как:
\[a_{\tau }=\frac{dv}{dt}=\frac{d^2s}{dt^2}\left(1.1\right).\]
Найдем первую производную от $s\left(t\right)=At^2+Bt$:
\[\frac{ds}{dt}=\frac{d}{dt}\left(At^2+Bt\right)=2At+B\ \left(1.2\right).\]
Вычислим вторую производную от $s\left(t\right)=At^2+Bt$:
\[\frac{d^2s}{dt^2}=\frac{d}{dt}\left(2At+B\right)=2А\left(1.3\right).\]
Мы получили, что:
\[a_{\tau }=2A\ne 0=const.\]
Ответ: Движение материальной точки в заданном случае не равномерное.
Пример 2
Задание: Найдите отношение ускорений двух материальных точек ($\frac{a_1}{a_2}$), которые равномерно движутся по окружностям, имеющим радиусы: $R_1\ и\ R_2\ (R_1\ >R_2)$ с одинаковыми скоростями.
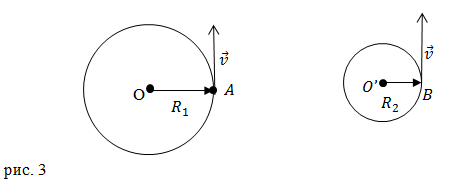
Решение: Так как точки движутся по окружностям с равномерно, то они будут иметь только центростремительные ускорения:
\[{\overline{a}}_1={\overline{a}}_{n1};;{\overline{a}}_2={\overline{a}}_{n2}\ \left(2.1\right),\]
которые направлены перпендикулярно вектору скорости в рассматриваемой точке и направлены к центру окружности. Модуль центростремительного ускорения при этом равен, для первой частицы:
\[a_{n1}=\frac{{v_1}^2}{R_1}\left(2.2\right),\]
для второй частицы:
\[a_{n2}=\frac{{v_2}^2}{R_2}\left(2.3\right).\]
Найдем отношение $\frac{a_1}{a_2}=\frac{a_{n1}}{a_{n2}}$, учтем, что по условию задачи:
\[v_1=v_2\left(2.4\right).\]
Получаем:
\[\frac{a_1}{a_2}=\frac{{v_1}^2}{R_1}:\frac{{v_2}^2}{R_2}=\frac{R_2}{R_1}.\]
Ответ: $\frac{a_1}{a_2}=\frac{R_2}{R_1}$
Читать дальше: сила упругости. Закон Гука.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 475 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!













