Движение тела под углом к горизонту, теория и онлайн калькуляторы
Движение тела под углом к горизонту
Начальные условия
Рассмотрим движение тела (материальной точки) брошенного под углом к горизонту с некоторой высоты $h_0$. Начальная
скорость тела равна ${\overline{v}}_0$, вектор ${\overline{v}}_0$ составляет угол $\alpha $ с горизонтом (рис.1). Систему отсчета, в которой движется тело, свяжем с Землей. Ось X направим параллельно земле, ось Y вертикально вверх.
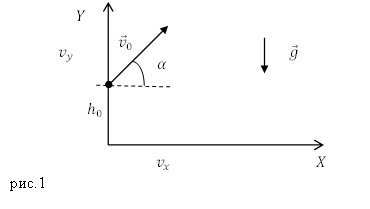
Движение тела под углом к горизонту происходит в поле тяжести Земли под воздействием силы тяжести. Силой сопротивления воздуха пренебрежём. В этом случае ускорение тела ($\overline{a}$) совпадает с ускорением свободного падения ($\overline{g}$):
\[\overline{a}=\overline{g}\left(1\right),\]
где $g=9,8\ \frac{м}{с^2}$.
Запишем начальные условия движения тела (рис.1):
\[\ \left\{ \begin{array}{c}
x\left(t=0\ \right)=0, \\
y\left(t=0\ \right)=h, \\
v_x\left(t=0\ \right){=v}_{0x}=v_0{\cos \alpha ,\ } \\
v_y\left(t=0\ \right){=v}_{0y}=v_0{\sin \alpha .\ } \end{array}
\right.\left(2\right).\]
Уравнение для перемещения тела, брошенного под углом к горизонту. Траектория его движения
Перемещение тела, которое бросили под углом к горизонту является равноускоренным, следовательно, для написания уравнения движения воспользуемся векторным уравнением для перемещения ($\overline{s}$) при равнопеременном движении в виде, учтем равенство (1):
\[\overline{s}(t)={\overline{s}}_0+{\overline{v}}_0t+\frac{\overline{g}t^2}{2}\left(3\right).\]
Векторное уравнение (3) в проекции на оси координат X и Y даст нам два скалярных уравнения:
\[\left\{ \begin{array}{c}
x(t)=v_0{\cos \alpha \ }t \\
y(t)=h_0+v_0{\sin \alpha \ }t-\frac{gt^2}{2} \end{array}
\right.\left(4\right).\]
Из системы уравнений (4) мы видим, что при рассматриваемом нами движении происходит наложение двух прямолинейных движений.
Причем по оси X тело под углом к горизонту движется с постоянной скоростью ${\ v}_{0x}=v_0{\cos \alpha ,\ }$ а по оси Y материальная точка перемещается с постоянным ускорением $\overline{g}$. Уравнение траектории движения тела можно получить, если из первого уравнения системы (4) выразить время ($t$) полученный результат подставить во вторую формулу системы:
\[t=\frac{x}{v_0{\cos \alpha \ }};;\ \]
\[y(x)=h_0\ tg\ \alpha -\frac{g}{2}{\left(\frac{x}{v_0{cos б\ }}\right)}^2\left(5\right).\]
Уравнение $y(x)$ (функция (5)) показывает, что тело движется по параболе в плоскости, в которой лежат векторы $\overline{g}$ и ${\overline{v}}_0.$
Уравнение скорости движения тела брошенного под углом к горизонту
В векторном виде уравнение для скорости движения рассматриваемого нами тела в произвольный момент времени запишем:
\[\overline{v}(t)={\overline{v}}_0+\overline{g}t\left(6\right).\]
В скалярном виде уравнение (6) представим в виде системы уравнений:
\[\left\{ \begin{array}{c}
v_x\left(t\right)=v_0{cos \alpha ,\ } \\
v_y\left(t\right)=v_0{sin \alpha \ }-gt \end{array}
\right.\left(7\right).\]
В системе уравнений (7) мы еще раз видим, что движение тела под углом к горизонту по оси X равномерное, по оси Y равнопеременное. Причем, двигаясь вверх, тело уменьшает свою скорость от $v_{0y}$ до нуля, затем падая вниз скорость тела увеличивается.
Модуль вектора скорости в производный момент времени для рассматриваемого нами движения найдем как:
\[v=\sqrt{v^2_x{+v}^2_y\ \left(8\right).}\]
Время подъема и полета тела
Время, которое тело тратит на полет вверх в рассматриваемом движении можно найти из второго уравнения системы (7). В точке максимального подъема вектор скорости точки параллелен оси X, значит $v_y=0$, тогда время подъема ($t_p$):
\[t_p=\frac{v_0{\sin \alpha \ }}{g}\left(9\right).\]
Время, которое тело находилось в воздухе (время полета($t_{pol}$)) получим из второго уравнения системы (4), приравняв ординату $y$ к нулю:
\[t_{pol}=\frac{v_0{\sin \alpha +\sqrt{v^2_0{sin}^2\alpha +2gh_0}\ }}{g}\left(10\right).\]
При $h_0=0$ мы видим, что $t_{pol}=2t_p.$
Дальность полета и высота подъема
Для того чтобы найти горизонтальную дальность полета тела ($s$) при заданных нами условиях в уравнение координаты $x$ системы уравнений (4) подставим время полета ($t_{pol}$) (10). При $h_0=0,$ дальность полета равна:
\[s=\frac{v^2_0{\sin \left(2\alpha \right)\ }}{g}\left(11\right).\]
Максимальную высоту подъема тела под углом к горизонту ($h_{max}$) находят из второго уравнения системы (4), подставляя в него время подъема ($t_p$) (9):
\[h_{max}=h_0+\frac{{v_0}^2{{sin}^2 б\ }}{2g}\left(12\right).\]
Примеры задач с решением
Пример 1
Задание. Каким будет угол ($\alpha $) под которым бросили тело к горизонту, если оказалось, что максимальная высота подъема ($h$) тела в четыре раза меньше, чем дальность его полета ($s$)? Сопротивление воздуха можно не учитывать.
Решение. Выберем систему отсчета связанную с Землей. Будем считать, что тело бросили из начала координат (рис.2).
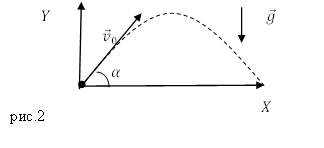
Запишем кинематические уравнения движения тела в поле тяжести земли:
\[\overline{s}(t)={\overline{s}}_0+{\overline{v}}_0t+\frac{\overline{g}t^2}{2}\left(1.1\right).\]
\[\overline{v}(t)={\overline{v}}_0+\overline{g}t\left(1.2\right)\]
Исходя из начальных условий, нашей задачи:
\[\left\{ \begin{array}{c}
{\overline{s}}_0=0 \\
v_{0x}=v_0{cos \alpha ,\ } \\
v_{0y}=v_0{sin \alpha \ } \end{array}
\right.\ \left(1.3\right).\]
В проекциях на оси уравнения (1.1) и (1.2)предстанут в виде:
\[\left\{ \begin{array}{c}
x(t)=v_0{cos \alpha \ }t \\
y(t)=v_0{sin \alpha \ }t-\frac{gt^2}{2} \end{array}
\right.\left(1.4\right).\]
\[\left\{ \begin{array}{c}
v_x\left(t\right)=v_0{cos \alpha ,\ } \\
v_y\left(t\right)=v_0{sin \alpha \ }-gt \end{array}
\right.\left(1.5\right).\]
Время подъема из второго уравнения системы (1.5) равно:
\[t_p=\frac{v_0{sin \alpha \ }}{g}\ \left(1.6\right).\]
Тогда максимальная высота подъема равна:
\[h=y\left(t_p\right)=\frac{v^2_0{sin}^2\alpha }{2g}\left(1.7\right).\]
Если тело бросили из начала координат, то $t_{pol}=2t_p,$ дальность полета найдем, подставив время полета в первое уравнение системы (1.4):
\[s=x\left(t_{pol}\right)=2v^2_0\frac{{{cos \alpha \ }sin \alpha \ }}{g}\ \left(1.8\right).\]
По условию задачи: $h=\frac{s}{4}$, используем уравнения (1.7) и (1.8):
\[\frac{v^2_0{sin}^2\alpha }{2g}=v^2_0\frac{{{cos \alpha \ }sin \alpha \ }}{2g}\to {\sin \alpha \ }={cos \alpha \ }\to \alpha =\frac{\pi }{4}.\]
Ответ. $\alpha =\frac{\pi }{4}$
Пример 2
Задание. Какова скорость падения тела брошенного под углом горизонта $\alpha $ со скоростью $v_0$? Если тело бросили с земли. Сопротивление воздуха можно не учитывать.
Решение. За основу решения задачи примем кинематическое уравнение для скорости движения тела в поле тяжести Земли:
\[\overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t\left(2.1\right).\]
Начальные условия движения нашего тела:
\[\left\{ \begin{array}{c}
{\overline{s}}_0=0 \\
v_{0x}=v_0{cos \alpha ,\ } \\
v_{0y}=v_0{sin \alpha \ } \end{array}
\right.\ \left(2.2\right).\]
В проекциях на оси X и Y уравнение (2.1):
\[\left\{ \begin{array}{c}
v_x\left(t\right)=v_0{cos \alpha ,\ } \\
v_y\left(t\right)=v_0{sin \alpha \ }-gt \end{array}
\right.\left(2.3\right).\]
Время подъёма тела, принимая во внимание, что $v_y\left(t_p\right)=0$ из второго уравнения (2.3) равно:
\[t_p=\frac{v_0{sin \alpha \ }}{g}\ \left(2.4\right).\]
Если тело бросили из начала координат, то $t_{pol}=2t_p:$
\[t_{pol}=\frac{2v_0{sin \alpha \ }}{g}\left(2.5\right).\]
Зная время полета, найдем $v_y\left(t_{pol}\right)$, подставив его во второе уравнение (2.3):
\[v_y\left(t_{pol}\right)=-v_0{sin \alpha \ \left(2.6\right).\ }\]
Модуль вектора скорости в момент падения найдем как:
\[v(t_{pol})=\sqrt{v^2_x{+v}^2_y\ }=v_0.\]
Ответ. При заданных условиях величина скорости падения равна модулю скорости бросания.
Читать дальше: динамика прямолинейного движения связанных тел.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 454 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!












