Равнодействующая всех сил, теория и онлайн калькуляторы
Равнодействующая всех сил
Мера взаимодействия тел - сила
В инерциальной системе отсчета изменение скорости тела может происходить только при его взаимодействии с другими телами. Для того чтобы охарактеризовать это взаимодействие используют такую физическую величину, как сила. Сила является количественной мерой взаимодействия.
С точки зрения физики природа взаимодействия тел может быть самой разной. Различают гравитационное, электрическое, магнитное и другие взаимодействия. При рассмотрении механического движения тела природа сил, которые изменяют скорость тела, не является существенной. Вопросом происхождения взаимодействия механика не занимается. Для всех видов взаимодействия количественной мерой является сила, силы разной природы измеряются в одних и тех же единицах, при помощи одних и тех же эталонов. Из-за данной универсальности механика успешно описывает движение тел на которые действуют силы любой природы.
И так, мерой взаимодействия тел или частиц служит такая векторная физическая величина как сила ($\overline{F}$). Результатом действия силы на тело является его деформация или изменение скорости перемещения, возможно и то и другое одновременно.
Сила - векторная величина. Равнодействующая всех сил
Имея в своем распоряжении градуированный динамометр экспериментально можно убедиться, что все силы, независимо от их природы, складываются как векторы.
Допустим, что на металлический шарик действуют две силы (рис.1): сила упругости со стороны пружины (${\overline{F}}_u$) и магнитная сила (${\overline{F}}_m$) со стороны постоянного магнита. Будем считать, что их значения измерены и известны. При совместном действии этих сил шарик будет находиться в состоянии покоя, если на него подействовать третьей силой ($\overline{F}$), которая будет удовлетворять равенству:
\[\overline{F}=-\left({\overline{F}}_u+{\overline{F}}_m\right)\left(1\right).\]
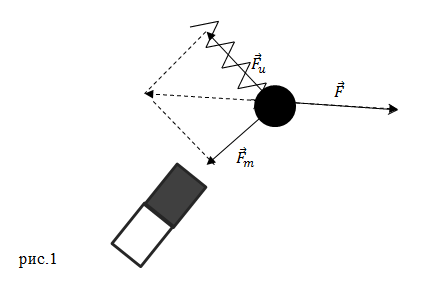
Описанный выше эксперимент позволяет сказать, что несколько сил, приложенных к одному телу можно заменять равнодействующей, не зависимо от их природы. Равнодействующая получается в результате векторного суммирования сил, воздействующих на тело.
Векторная сумма всех сил, действующих на тело одновременно, называется равнодействующей силой ($\overline{F}$):
\[\overline{F}={\overline{F}}_1+{\overline{F}}_2+\dots +{\overline{F}}_N=\sum\limits^N_{i=1}{{\overline{F}}_i}\ \left(2\right).\]
Иногда равнодействующую силу обозначают $\overline{R}$, чтобы выделить, но это не обязательно.
Графически равнодействующую можно найти по правилу многоугольника, параллелограмм и треугольника. Если при таком сложении сил многоугольник получился замкнутым, то равнодействующая равна нулю. При равенстве нулю равнодействующей систему называют уравновешенной.
Второй закон Ньютона
Основным законом в классической динамике является второй закон Ньютона, который связывает силы, оказывающие воздействие
на тело и его ускорение. В том случае, если на тело оказывают воздействие несколько сил, то второй закон Ньютона формулирую так:
\[\overline{R}=\sum\limits^N_{i=1}{{\overline{F}}_i}=m\overline{a}\left(3\right).\]
Равнодействующая всех сил, действующих на тело, может быть равна нулю, в том случае, если происходит взаимная компенсация сил, приложенных к телу. В таком случае тело движется с постоянной скоростью или находится в покое. Можно сказать обратное, если тело движется равномерно и прямолинейно в инерциальной системе отсчета, то на него не действуют силы или их равнодействующая равна нулю.
При решении задач и изображении сил, действующих на тело, на рисунке, если тело движется с постоянным ускорением, равнодействующую силу направляют по ускорению и изображают длиннее, чем противоположно ей направленную силу (сумму сил). При равномерном движении (или если тело находится в состоянии покоя) длина векторов сил, имеющих противоположные направления одинакова.
Изучая условия задачи, следует выяснить, какие силы действуют на тело, и войдут в равнодействующую, какие силы не оказывают существенного влияние на движение тела и их можно не учитывать. Значимые силы изображают на чертеже. Складывают силы по правилам сложения векторов.
Примеры задач на равнодействующую сил
Пример 1
Задание: Найдите равнодействующую сил, представленных на рис.2.
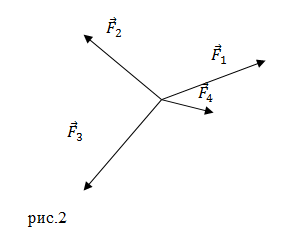
Решение: Сложим силы, применяя правило многоугольника. Последовательно каждый следующий вектор силы отложим от конца предыдущего. В результате вектор равнодействующей всех сил будет иметь началом точку, из которой выходит первый вектор (у нас вектор ${\overline{F}}_1$), ее конец будет приходить в точку, где заканчивается последний вектор (${\overline{F}}_4$). В результате получим рис.3.
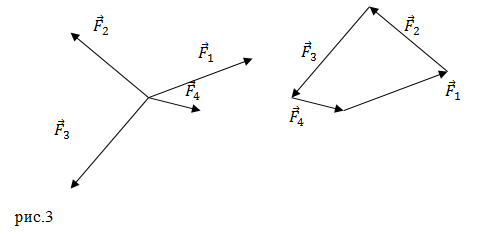
Мы получили замкнутый многоугольник, следовательно, равнодействующая сил равна нулю.
Ответ: $\overline{R}=0$
Пример 2
Задание: Материальная точка массы $m$ движется так, что закон ее движения записывается уравнением: $s=A{\cos (\omega t)(м)\ }$, где $s$ - путь пройденный точкой; $A=const;;\ \omega =const.$ Запишите закон изменения величины равнодействующей силы, действующей на точку ($F(t)$).\textit{}
Решение: В соответствии со вторым законом Ньютона равнодействующая сил, приложенных к материальной точке равна:
\[\overline{F}=m\overline{a}\left(2.1\right).\]
Ускорение точки найдем как:
\[a=\frac{d^2s}{dt^2}\left(2.2\right).\]
Найдем первую, а за тем вторую производные от $x$ по времени:
\[\frac{ds}{dt}=\frac{d}{dt}(A{cos (\omega t))=-A\omega \ {\rm sin}?(\omega t)\ (м)\ }\left(\frac{м}{с}\right);;\frac{d^2s}{dt^2}=-A{\omega }^2{\cos \left(\omega t\right)\ }\ \left(\frac{м}{с^2}\right)(2.3).\]
Используя результат (2.3), выражение для равнодействующей силы запишем как:
\[F=-mA{\omega }^2{cos \left(\omega t\right)\ }\left(Н\right).\]
Ответ: $F=-mA{\omega }^2{cos \left(\omega t\right)\ }\left(Н\right)$
Читать дальше: равномерное движение по окружности.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 469 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!













