Затухающими колебаниями называют колебания, амплитуда которых постепенно уменьшается со временем из-за потерь энергии колебательной системой.
Затухающие колебания
Определение затухающих колебаний
Механическое движение всегда сопровождается трением. Трение приводит к рассеянию (диссипации) механической энергии. Диссипация энергии имеется в любых не идеализированных колебательных системах, она вызывает затухание собственных колебаний.
Уравнение колебаний пружинного маятника с затуханием
Иногда, если тело движется в веществе, силу сопротивления (${\overline{F}}_{tr}$), которая действует на рассматриваемое тело, при маленьких скоростях его движения, считают прямо пропорциональной скорости ($\overline{v}$):
\[{\overline{F}}_{tr}=-\beta \overline{v}\left(1\right),\]где $\beta $ - коэффициент сопротивления.
Данную силу учитывают в уравнении второго закона Ньютона при описании движения. Так, уравнение, которое описывает линейные колебания по вертикали (колебания по оси X) пружинного маятника, учитывающее силу трения принимает вид:
\[m\ddot{x}=-kx-\beta \dot{x}\left(2\right),\]где $\dot{x}=v_x.$ Принимая во внимание равенства:
\[{\omega }^2_0=\frac{k}{m};;2\gamma =\frac{\beta }{m}\left(3\right),\](где ${\omega }_0$- циклическая частота свободных незатухающих колебаний (собственная частота колебаний при $\gamma $=0) той же колебательной системы; $\gamma $ - коэффициент затухания) уравнение колебаний пружинного маятника с затуханием (2) преобразуем к виду:
\[\ddot{x}+2\gamma \dot{x}+{\omega }^2_0x=0\ \left(4\right).\]Малые собственные колебания, затухающие вследствие сопротивления среды в любой физической системе (математический маятник, физический маятник, электрические колебания ...) описывают при помощи уравнения формы (4).
Уравнение затухающих колебаний имеет точное решение:
\[x\left(t\right)=A_0e^{-\gamma t}{\cos \left(\omega t+\varphi \ \right)\left(5\right),\ }\]где $\omega =\sqrt{{\omega }^2_0-{\gamma }^2}$; $A_0$ - начальная амплитуда колебаний, задаваемая начальными условиями; $\varphi $ - постоянная из начальных условий. При $\gamma \ll {\omega }_0$, $\omega \approx {\omega }_0$, параметр $A_0e^{-\gamma t}$ можно считать медленно изменяющейся во времени амплитудой колебаний.
Затухание колебаний по экспоненте связано с тем, что силу сопротивления мы приняли пропорциональной скорости. Если использовать другую зависимость силы трения от скорости, то закон затухания изменится.
Диссипация энергии при затухающих колебаниях
Пусть затухание мало, при этом потеря энергии колебательной системой за один период много меньше, чем энергия колебаний.
Рассеяние энергии за период колебаний происходит не равномерно, ввиду осцилляции кинетической энергии ($E_k$). Уравнение убывания энергии при затухающих колебаниях будет иметь вид:
\[\frac{dE}{dt}=-\frac{2\beta }{m}\left\langle E_k\right\rangle \left(6\right),\]где $\frac{dE}{dt}$ - скорость изменения энергии колебаний; $\left\langle E_k\right\rangle $ - средняя величина кинетической энергии за период колебаний. Уравнение (6) не применяют для промежутков времени, которые меньше периода колебаний.
Так как мы считаем затухание малым, то $\left\langle E_k\right\rangle $ можно принять равным (как при свободных колебаниях) половине полной энергии осциллятора:
\[\left\langle E_k\right\rangle =\frac{E}{2}\left(7\right).\]В таком случае уравнение (6) можно записать в виде:
\[\frac{dE}{dt}=-2\gamma E\ \left(8\right).\]Выражение (8) отображает «сглаженное» поведение энергии колебаний (в случае, если детали изменения энергии за один период колебаний не интересны). Оно показывает, что скорость изменения энергии пропорциональна самой энергии. Решением уравнения (8) является функция:
\[E\left(t\right)=E_0e^{\left(-2\gamma t\right)}\left(9\right),\]где $E_0$ - величина энергии колебательной системы в начальный момент времени.
Так как энергия колебаний пропорциональна квадрату амплитуды ($E\sim A^2$), изменение амплитуды колебаний за большие отрезки времени (в сравнении с периодом колебаний) запишем в виде функции:
\[A=A_0e^{-\gamma t}\left(10\right),\]$A_0$ - начальная амплитуда колебаний.
Время жизни колебаний. Период затухающих колебаний. Декремент затухания
Из формулы (10) видно, что амплитуда затухающих колебаний убывает по экспоненте. За время $\tau =\frac{1}{\gamma }$ амплитуда убывает в $e$ раз и это не зависит от $A_0$. Время $\tau $ в этом случае называют временем жизни колебаний (или временем релаксации) (не смотря на то, что в соответствии с выражением (9) колебания должны длиться бесконечно). Тезис о малости затухания означает, что время жизни колебаний не бесконечно, а много больше, чем их период ($\tau \gg T$). За время жизни происходит много колебательных движений.
Строго говоря, затухающие колебания не являются строго периодическими движениями. Периодом в данном случае считают промежуток времени между двумя последовательными максимальными отклонениями от положения равновесия.
Период затухающих колебаний считают равным:
\[T=\frac{2\pi }{\sqrt{{\omega }^2_0-{\gamma }^2}}\left(11\right).\]Пусть $A\left(t\right)\ и\ A(t+T)$ - амплитуды двух последовательных колебаний, моменты времени которых отличаются на период. Отношение этих амплитуд, следуя (10) равно:
\[\frac{A\left(t\right)}{A(t+T)}=e^{\gamma T}(12)\]называют декрементом затухания. Натуральный логарифм декремента затухания ($\theta $):
\[\theta ={\ln \left(\frac{A\left(t\right)}{A\left(t+T\right)}\right)\ }=\gamma T=\frac{T}{\tau }=\frac{1}{N_e}(13)\]называют логарифмическим декрементом затухания. Для колебательной системы $\theta $ постоянная величина.
Примеры задач с решением
Задание. Каков коэффициент затухания маятника ($\gamma $), если за $\Delta t$ амплитуда его колебаний уменьшилась в $n$ раз?
Решение. За основу решения задачи примем уравнение затухающих колебаний в виде:
\[x\left(t\right)=A_0e^{-\gamma t}{\cos \left(\omega t+\varphi \ \right)\left(1.1\right),\ }\]По условию задачи имеем:
\[\frac{A_1}{A_2}=n.\]С другой стороны:
\[A_1\left(t_1\right)=A_0e^{-\gamma t_1};;A_2\left(t_2\right)=A_0e^{-\gamma t_2}\ \to \frac{A_1}{A_2}=\frac{A_0e^{-\gamma t_1}}{A_0e^{-\gamma t_2}}=e^{\gamma \Delta t}\left(1.2\right),\]где $t_2-t_1=\Delta t$. Найдем натуральный логарифм от правой и левой части выражения (1.2), получим:
\[{\ln \left(\frac{A_1}{A_2}\right)\ }=\gamma \Delta t\left(1.3\right).\]Выразим $\gamma $ из (1.3) учтем, что $\frac{A_1}{A_2}=n$:
\[\gamma =\frac{{\ln \left(\frac{A_1}{A_2}\right)\ }}{\Delta t}=\gamma =\frac{{\ln n\ }}{\Delta t}.\]Ответ. $\gamma =\frac{{\ln n\ }}{\Delta t}$
Задание. Что представляет собой фазовая траектория затухающего колебания?
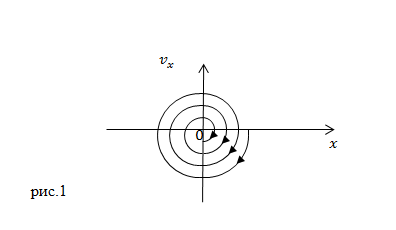
Решение. Фазовой траекторией называют траекторию движения в плоскости $\left(x;;v\right).$ По оси абсцисс откладывается отклонение $x$, по оси ординат откладывают скорость $v$. Каждому движению в момент времени $t$ соответствует изображающая точка, на указанной плоскости координаты ее $\left(x,v\right),$ они однозначно определены мгновенными значениями отклонения и скорости. Точка со временем движется и описывает траекторию (рис.1). В данном случае время выступает как параметр, уравнение фазовой траектории задет функция:
\[v=v\left(x\right)\left(2.1\right).\]Фазовая траектория затухающего колебания, если
\[{\overline{F}}_{tr}=-\beta \overline{v}\left(2.2\right),\]представляет собой незамкнутую спираль, которая закручивается вокруг начала координат (рис.1). Если затухание колебаний малое, то есть за время жизни колебательная система совершает множество колебаний, количество витков спирали в фазовой плоскости будет таким же.
Читать дальше: линейная скорость.










