Деформация тела - это изменение его размеров или формы.
Сила упругости
Природа сил упругости
Как известно все тела состоят из атомов и молекул, которые строятся из ядер и электронов, несут электрические заряды. Между заряженными частицами действуют силы электрического взаимодействия, при этом одноименно заряженные частицы отталкиваются, частицы противоположных знаков притягиваются. Величина этих сил зависит от расстояний между частицами. На расстояниях около диаметра молекулы силы притяжения между молекулами компенсированы силами отталкивания, то есть равнодействующая сил притяжения и отталкивания равна нулю. Если тело растягивать, то расстояние между молекулами увеличивается, при этом силы притяжения между молекулами становятся больше по величине, чем силы отталкивания. В теле появляются силы, которые препятствуют растяжению тела. При сжимании тела расстояние между молекулами уменьшается. Силы отталкивания становятся по модулю больше, чем силы притяжения, так возникают силы, противостоящие такого рода деформации тела.
Так, при деформации тел появляются силы электромагнитной природы, которые препятствуют изменению размеров тела, это так называемые силы упругости.
Силы упругости и деформация тела
Определение
К деформациям относят: растяжение, сжатие, сдвиг, изгиб, кручение. Деформация появляется тогда, когда происходит перемещение одних частей тела относительно других.
Силы упругости появляются исключительно при деформациях. Величина силы упругости связана с размером деформации. Силы упругости имеют направление противоположное направлению смещения частиц тела при его деформации. Допустим, что к вертикальной пружине подвесили груз. Тогда на груз со стороны пружины будет действовать сила упругости.
Определение силы упругости
Определение
Силой упругости (${\overline{F}}_{upr}$) называют силу, которая действует со стороны тела подвергшегося деформации, на касающиеся его тела, она направлена в сторону, противоположную смещению частей тела в состоянии деформации.
Силы упругости определяются расположением взаимодействующих тел и появляются только при их деформациях.
Силы упругости направлены нормально поверхности соприкосновения взаимодействующих тел. Но при наличии деформации сдвига силы упругости обладают и касательную компоненту.
Если деформирующая сила равна нулю, то сила упругости так же будет равна нулю.
Не всегда деформации приводят к возникновению сил упругости. Существуют упругие тела, которые полностью восстанавливают свою форму и размер после снятия деформации. Такие деформации называют упругими, в них возникают силы упругости. Есть тела, которые после прекращения действия деформирующей силы не восстанавливают (или восстанавливают не полностью) свои размеры и форму, такие тела называют пластичными, а деформации пластическими. В таких деформациях сил упругости не возникает.
Закон Гука
Эмпирическая зависимость силы упругости от величины деформации была установлена во времена И. Ньютона английским ученым Р. Гуком. Закон упругой деформации назван по имени своего первооткрывателя. Этот закон выполняется только для малых упругих деформаций. Закон Гука утверждает, что при малых упругих деформациях величина деформации пропорциональна силе ее вызывающей. Закон Гука выполняется для разных видов упругой деформации (растяжения, сжатия, сдвига, кручения, изгиба).
Так, деформацию растяжения (сжатия) принято характеризовать при помощи абсолютного удлинения ($\Delta l=\left|l-l_0\right|$, где $l_0$ - длина недеформированного стержня). Закон Гука относительно сил упругости формулируют как:
\[F_{upr}=k\Delta l\ \left(1\right).\]где $k$ - коэффициент упругости (коэффициент жесткости, жесткость), $\left[k\right]=\frac{Н}{м}$. Коэффициент упругости зависит от материала тела, его размеров и формы.
Закон Гука хорошо работает для деформаций, которые возникают в стержнях из стали, чугуна, и других твердых веществ, в пружинах. Справедлив закон Гука для деформаций растяжения и сжатия.
Если деформации тела малы, то силы упругости можно определять по ускорению, которое данные силы сообщают телам. Если тело неподвижно, то модуль силы упругости находят из равенства нулю векторной суммы сил, которые действуют на тело.
При больших деформациях линейной зависимости между величиной деформации и силами нет.
Примеры задач с cилой упругости
Пример 1
Задание. Два тела одинаковой массы соединяет невесомая пружина, коэффициент упругости которой равен $k$. Тела скользят с ускорением по абсолютно гладкой горизонтальной поверхности за счет горизонтальной силы $\overline{F}$, которая приложена к одному из грузов (рис.1). Каково удлинение пружины?
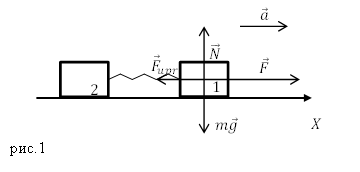
Решение. Рассмотрим силы, которые приложены к первому грузу, запишем второй закон Ньютона для него:
\[m\overline{g}+\overline{N}+\overline{F}+{\overline{F}}_{upr}=m\overline{a}\left(1.1\right).\]Запишем проекцию выражения (1.1) на ось X:
\[F-F_{upr}=ma\ \left(1.2\right).\]Определим, какие силы действуют на систему, которая состоит сразу из двух грузов (первого и второго). Это сила тяжести (2$\ m\overline{g}$); сила реакции опоры ($\overline{N}'$); сила тяги $\left(\overline{F}\right).$ Запишем второй закон Ньютона:
\[\ m\overline{g}+{\overline{N}}'+\overline{F}=2m\overline{a}\left(1.3\right).\]В проекции выражения (1.3) на ось X, получим:
\[F=2ma\ \left(1.4\right).\]Выразим из (1.4) ускорение и подставим его в (1.2):
\[F-F_{upr}=ma=m\cdot \frac{F}{2m}\to F_{upr}=\frac{F}{2}\left(1.5\right).\]Считая деформацию пружины небольшой и упругой, используем закон Гука, для определения силы упругости:
\[F_{upr}=k\Delta l=\frac{F}{2}\left(1.6\right).\]Выразим удлинение пружины из (1.6):
\[\Delta l=\frac{F}{2k}.\]Ответ. $\Delta l=\frac{F}{2k}$
Пример 2
Задание. Могут ли возникать силы упругости в жидкостях и газах?
Решение. Силы упругости возникают при наличии упругих деформаций. Твердые тела сохраняют форму и объем, если пытаться их деформировать появляются силы упругости.
Жидкости не сохраняют свою форму, но сохраняют объем. Если пытаться сжать жидкость, тот сила упругости возникает.
Газ, находящийся в замкнутом сосуде всегда сжат и всегда обладает упругостью.
Читать дальше: сила.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
Статьи по теме
Поможем выполнить
любую работу
