Звуковыми (акустическими) волнами называют упругие волны, распространяющиеся в среде, имеющие частоты в диапазоне $16\le \nu \le 20~000\ $Гц.
Звук
Определение и основные понятия звуковых волн (звука)
Оказывая воздействие на слуховой аппарат человека, такие волны вызывают ощущение звука. Волны, частоты которых меньше 16 Гц, называют инфразвуковыми. Волны, имеющие частоту больше, чем 20~000 Гц называют ультразвуковыми. Инфразвук и ультразвук человек не слышит.
Волны звука в газах и жидкостях могут быть только продольными, потому что эти вещества имеют упругость только по отношению к сжатию (растяжению). В твердых телах волны звука могут быть и продольными и поперечными, так как твердые тела могут быть упругими по отношению к деформациям сжатия (растяжения) и сдвига.
Характеристики звуковых волн
Интенсивностью звука (силой звука) ($I$) называют величину, которую определяют средней по времени энергией ($\left\langle E\right\rangle $), переносимой волной звука за единицу времени, через единичную площадку, нормальную к направлению распространению волны:
\[I=\frac{\left\langle E\right\rangle }{St}\left(1\right).\]Единицей измерения силы звука служит в Международной системе единиц (СИ) ватт деленный на квадратный метр:
\[\left[I\right]=\frac{Вт}{м^2}.\]Для того чтобы человек слышал звук, волна звука должна иметь некую минимальную интенсивность, но если сила звука превысила некоторый предел, то человек звук не слышит, но ощущает боль. Для каждой частоты колебаний существует наименьшая (пороговая слышимость) и наибольшая (порог болевых ощущений) сила звука, которую человек способен воспринимать.
Громкость звука - это субъективная характеристика звука, которая связана с его силой. Громкость звука зависит от частоты. По закону из физиологии, при увеличении интенсивности звука его громкость растет по закону логарифма. На этом основании вводится объективная оценка громкости звука:
\[L={\lg \left(\frac{I}{I_0}\right)\ }\left(2\right),\]где $I_0$ - интенсивность звука на пороге слышимости, для всех звуков ${10}^{-12}\frac{Вт}{м^2}$; $L$ - уровень интенсивности звука. Единицей измерения $L$ является бел (Б). Чаще используют такую единицы уровня интенсивности звука как децибел (дБ), он в 10 раз меньше, чем бел.
Уровень громкости - физиологическая характеристика звука, единицей измерения которой, является фон. Громкость для звука 1000 Гц (частота стандартного тона) составляет 1 фон, если его уровень интенсивности 1 дБ. Так, шепот на расстоянии один метр имеет уровень громкости примерно 20 фон.
Звук в действительности представляет собой наложение гармонических колебаний большим набором частот. При этом говорят, что звук имеет акустический спектр. Этот спектр может быть сплошным или линейчатым. В линейчатом спектре имеются отделенные друг от друга частоты.
Высота звука - это качество звука, которое человек определяет субъективно на слух. Высота звука зависит от его частоты. С увеличением частоты высота звука увеличивается.
Тембром звука называют звуковое ощущение, которое определяет характер акустического спектра и распределения энергии между определенными частотами.
Любое тело, совершающее колебания в упругой среде с частотой звука может стать источником звуковых волн. Колеблющееся тело вызывает колебания частичек среды, в котором оно находится с частотой колебаний тела. В веществе распространяется волна, имеющая частоту источника колебаний. Скорость ($v$) распространения волны зависит от плотности и упругих свойств вещества. Для газа она равна:
\[v=\sqrt{\frac{\gamma RT}{\mu }}\left(3\right),\]где $\gamma =\frac{c_{\mu p}}{c_{\mu V}}$; $c_{\mu p}$ -молярная теплоемкость газа при постоянном давлении; $c_{\mu V}$ - молярная теплоемкость газа при постоянном объеме; $R$ - универсальная газовая постоянная; $T$ - температура; $\mu $ - молярная масса. Формула (3) является идеализированной. Так, при распространении звука в атмосфере следует учесть скорость и направление ветра, влажность воздуха, преломление и отражение волн на границе сред, вязкость.
Если источник и приёмник звука находятся в состоянии покоя относительно среды, то длина волны звука равна:
\[\lambda =vT=\frac{v}{\nu }\left(4\right),\]где $v$ - скорость распространения волны в веществ; $\nu $ - частота звука.
Примеры задач с решением
Задание. Какова интенсивность звука, если уровень его интенсивности равен $L=67$дБ? Интенсивность звука, на пороге слышимости составляет ${I_0=10}^{-12}\frac{Вт}{м^2}$.
Решение. Основой для решения задачи нам будет служить формула для уровня интенсивности звука:
\[L={\lg \left(\frac{I}{I_0}\right)\ }\left(1.1\right).\]Выразим из нее интенсивность звука:
\[\frac{I}{I_0}={10}^L\to I={10}^L\cdot I_0.\]Переведем $L=67$дБ=6,7 Б, вычислим искомую величину:
\[I={10}^{6,7}\cdot {10}^{-12}\approx 5\cdot {10}^{-6}\left(\frac{Вт}{м^2}\right).\]Ответ. $I=5\cdot {10}^{-6}\frac{Вт}{м^2}$
Задание. На рис.1 изображена река. Скорость движения воды в реке равна $v_0$. В воде установлен источник звуковых колебаний с частотой ${\nu }_0$. На двух берегах реки на равных расстояниях установлены неподвижные приемники колебаний (1 и 2). Какую частоту звука зарегистрируют приемники?
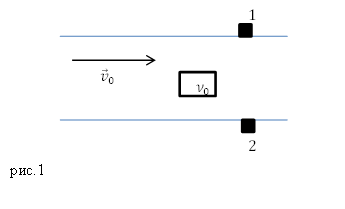
Решение. Пусть скорость распространения звуковой волны в воде равна $v$, то длина волны:
\[\lambda =vT=\frac{v}{{\nu }_0}\left(2.1\right).\]Рассмотрим первый приемник. При распространении в воде, волна достигнет приемника и вызовет колебания его звукочувствительного элемента с частотой, равной:
\[{\nu }_1=\frac{v}{\lambda }=\frac{v}{vT}={\nu }_0.\]Частота звука, регистрируемого приемником равна частоте, которою испускает источник.
Ответ. ${\nu }_1={\nu }_2={\nu }_0$
Читать дальше: импульс тела.










